Summary

WolframAlpha has a useful function called cryptograms which, given a word enciphered in a simple substitution alphabet, returns all possible English words that the enciphered word could represent. I thought it would be even more useful to be able to enter a list of ciphertext words (assumed to be enciphered in the same substitution alphabet), and get a list of all possible English words that could be represented by those words. An example might be "cryptograms UMVUYM QRZMSFRN". This would give a list like {{people, asterisk}, {people, asterism}, ..., {proper, snarling},..., {proper, unarming}, ...}. The word pairs not only match the patterns of the enciphered words, but are also consistent with an enciphering alphabet. Since WolframAlpha's cryptograms function does not have this functionality, I decided to implement it in Mathematica.

Note that this program is not intended to solve cryptograms automatically (the way this program from the Wolfram Demonstrations Project does). I think of it more as a tool to aid in the solution of more difficult problems.

Introduction

In a simple substitution cipher, plaintext letters are replaced by ciphertext letters according to an enciphering rule. For example given the rule {p $\rightarrow$ U, e $\rightarrow$ M, o $\rightarrow$ V, l $\rightarrow$ Y} the word people becomes UMVUYM (here I use the convention that plaintext letters are lowercase and ciphertext letters are uppercase). The resulting ciphertext, presented without the enciphering rule, is sometimes called a cryptogram. The objective is to reconstruct the enciphering rule and read the original plaintext. An example cryptogram is:

UWJPQTHB ZVCWFUOPQGN FEHPBNOGDX RGTHQNZVPF JWQMYZS TWQPNZFV

The Wolfram Alpha function cryptograms is a useful aid in solving short cryptograms like this. For example, given ciphertext word UMVUYM, Wolfram Alpha returns:

WolframAlpha["cryptograms UMVUYM"]

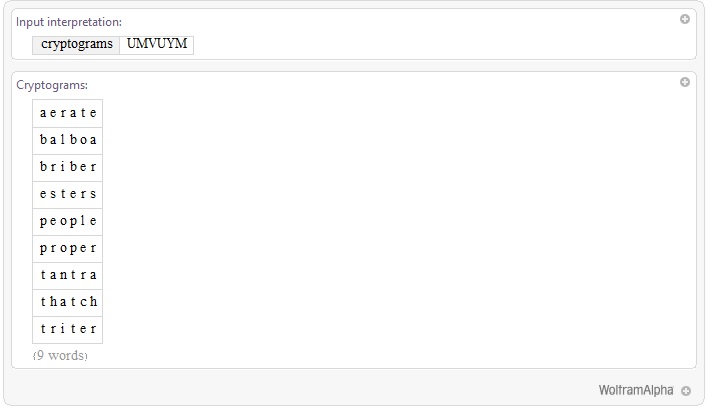
Basically the function gives a list of all six-letter English words that have the first and fourth letters the same, the second and sixth the same, and no other repeats. Experienced solvers will recognize people as the most likely word on the list. If that doesn't lead to the solution of a given cryptogram, it would not be difficult to try each of the remaining 8 possibilities.

Unfortunately, in many cases the list of words produced is much longer. For example:

WolframAlpha["cryptograms QRZMSFRN"]

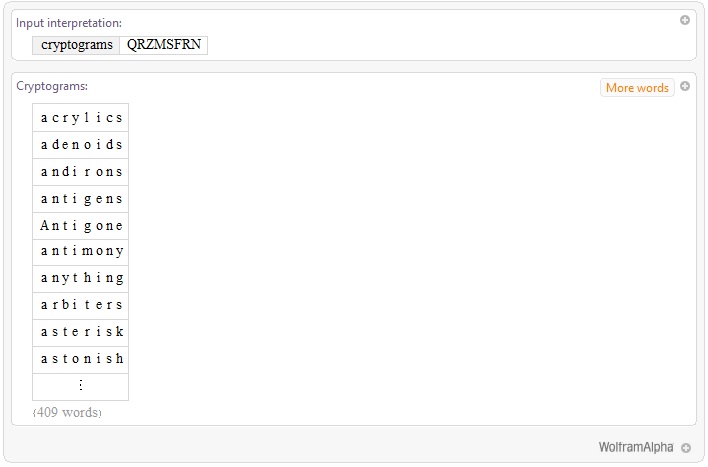
Here we get a list of eight-letter words in which the second and seventh letters are the same and there are no other repeats. There are 409 such words -- far more than can be checked by hand. But it occurred to me that if it were possible to cross-index the lists generated for two or more ciphertext words, the number of possible solutions could be shortened considerably.

What I mean by cross-index is this: Assume that UMVUYM and QRZMSFRN both come from the same cryptogram. Given the two lists of possible words: {aerate, balboa, briber, esters, laelia, people, proper, tantra, thatch, triter} and {acrylics, adenoids, anderons, ..., zirconia}, there are 9x409 = 3,681 word pairs representing possible solutions. The first pair is {aerate, acrylics}. Are these two words compatible with UMVUYM and QRZMSFRN? No, because the first implies U $\rightarrow$ a and the second implies Q $\rightarrow$ a. The second pair, {aerate, anderons} leads to a similar contradiction.

Automating the Process

Unfortunately, I can't get the Wolfram Language to disclose the code behind cryptograms. This is supposed to work, but it fails:

WolframAlpha["cryptograms UMVULM", "WolframParse"]

So I needed to write my own version. I began with the following function, which finds the position of repeated letters in a word:

pattern[wrd_String] := 
 StringPosition[wrd, #][[All, 1]] & /@ 
  Select[Tally[Characters[wrd]], #[[2]] > 1 &][[All, 1]]

We know that the word people has the first and fourth letters the same, and the second and sixth letters the same. That's exactly what this function returns:

pattern["people"]

{{1, 4}, {2, 6}}

Note that since non-repeated letters at the end of a word do not affect the output of pattern ...

pattern["peopled"]

{{1, 4}, {2, 6}}

...we still have to check if candidate plaintext words have the same length as the ciphertext word. Here then is a function that generates a list of English words compatible with a given ciphertext word:

wordList[wrd_String] := 
With[{pat = pattern[wrd], len = StringLength[wrd]}, 
Select[WordList["KnownWords", IncludeInflections -> True], 
If[StringLength[#] != len, False, SameQ[pattern[#], pat]] &]]

This operates just like WolframAlpha's cryptogram function: Given a ciphertext word, the function checks every word in the dictionary sequentially to see whether it has the same length and pattern as the ciphertext word, and returns a list of those that do. We can try this out with a ciphertext word like XJXDRWX, which I just made up:

wordList["XJXDRWX"]

{"acantha", "acapnia", "acardia", "amastia", "anaemia", "elegise", \
"elegize", "elevate", "epergne", "eremite", "execute", "eyehole", \
"eyelike", "eyesore", "sisters", "susliks", "systems"}

Now we need a function that checks if a list of plaintext words is compatible with a list of ciphertext words:

compatible[cw_List, pw_List] := 
 Module[{cta = <|{}|>, pta = <|{}|>, ct = Characters[StringJoin[cw]], 
   pt = Characters[StringJoin[pw]]}, 
  Catch[MapThread[
    If[KeyFreeQ[cta, #1], cta = Join[cta, <|#1 -> #2|>], 
      If[cta[#1] != #2, Throw[False]]]; 
     If[KeyFreeQ[pta, #2], pta = Join[pta, <|#2 -> #1|>], 
      If[pta[#2] != #1, Throw[False]]]; &
    , {ct, pt}]; True]]

What I'm doing here is building the enciphering rule and its inverse one letter at a time using MapThread. If any ciphertext letter is found to correspond to two different plaintext letters -- or if any plaintext letter is found to correspond to two different ciphertext letters -- then we know the list of plaintext words is incompatible with the list of ciphertext words. The function throws an exception, exits immediately and returns the value False. Otherwise if we get to the end of the strings and no exception was thrown, the lists are compatible and the function returns True.

For example:

compatible[{"UMVULM", "QRZMSFRN"}, {"people", "asterisk"}]

True

compatible[{"UMVULM", "QRZMSFRN"}, {"people", "antimony"}]

False

The previous list is incompatible because the first word implies M $\rightarrow$ e and the second word implies M $\rightarrow$ i.

Now, finally, we can write a function to cross-index lists of possible words corresponding to a list of ciphertext words:

cryptograms[ctwords_List] := 
 Module[{ptwords, lst}, ptwords = wordList /@ ctwords; 
  lst = Tuples[ptwords]; Select[lst, compatible[ctwords, #] & ]]

Let's go back to the cryptogram presented at the beginning of this post:

ctext = "UWJPQTHB ZVCWFUOPQGN FEHPBNOGDX RGTHQNZVPF JWQMYZS TWQPNZFV";

Obviously the running time of the function cryptograms depends on the number of possible plaintext words corresponding to each ciphertext word, so let's find the length of each list:

ctext = StringSplit[ctext];
Length /@ wordList /@ ctext
{4194, 321, 1028, 1028, 6018, 4194}

This suggests that checking the second and third words (or the second and fourth) would have the shortest running time:

cryptograms[{ctext[[2]], ctext[[3]]}]
{{"atmospheric", "squelching"}}

So there is only one possibility in the dictionary for these two ciphertext words. They can only be atmospheric and squelching. Knowing these two is enough to make a good start at solving what would otherwise be a very difficult cryptogram.

Unfortunately we don't always get such clear answers. The original two words UMVUYM and QRZMSFRN return a list of 68 possible pairs:

cryptograms[{"UMVUYM", "QRZMSFRN"}]

 {{"aerate", "Angevins"}, {"aerate", "cohesion"}, {"aerate", "Numenius"}, 
{"aerate", "Poseidon"}, {"aerate", "unsexing"}, 
{"balboa", "decanter"}, {"balboa", "deranges"},
{"balboa", "detaches"}, {"balboa", "encasing"},
{"balboa", "escapism"}, {"balboa", "escapist"}, 
{"balboa", "kneading"}, {"balboa", "Picardie"}, 
{"balboa", "recanted"}, {"balboa", "regained"}, 
{"balboa", "remained"}, {"balboa", "retained"}, 
{"balboa", "revamped"}, {"balboa", "rifampin"}, 
{"balboa", "scraunch"}, {"balboa",  "sneaking"}, 
{"balboa", "treasury"}, {"balboa", "Treasury"}, 
{"balboa", "uncaring"}, {"balboa", "uncasing"}, 
{"balboa", "unfading"}, {"balboa", "unmaking"}, 
{"balboa", "unsaying"}, {"briber", "Hydromys"},
{"briber", "hydroxyl"}, {"briber", "madronas"}, 
{"briber", "touracos"}, {"esters", "flashily"}, 
{"laelia", "runabout"}, {"laelia", "scraunch"}, 
{"laelia", "turacous"}, {"people", "Angevins"}, 
{"people", "asterisk"}, {"people", "asterism"}, 
{"people", "Bayesian"}, {"people", "cadenzas"}, 
{"people", "Hibernia"}, {"people", "Jamesian"}, 
{"people", "Madeiras"}, {"people", "magentas"}, 
{"people", "Numenius"}, {"people", "strength"}, 
{"people", "unsexing"}, {"people", "waterman"}, 
{"proper", "dairyman"}, {"proper", "madrigal"}, 
{"proper", "snarfing"}, {"proper", "snarling"}, 
{"proper", "unarming"}, {"tantra", "becalmed"}, 
{"tantra", "behalves"}, {"tantra", "bewailed"}, 
{"tantra", "debacles"}, {"tantra", "devalues"}, 
{"tantra", "escapism"}, {"tantra", "Islamise"}, 
{"tantra", "legacies"}, {"tantra", "limacoid"}, 
{"thatch", "Burhinus"}, {"thatch", "keyholes"}, 
{"triter", "Hydromys"}, {"triter", "hydroxyl"}, 
{"triter", "madronas"}}

However given a third word FMSMZKRM from the same cryptogram , we do get a single result:

cryptograms[{"UMVUYM", "FMSMZKRM", "QRZMSFRN"}]
{{"people", "generate", "strength"}}

Others can undoubtedly improve on these functions. Obviously if we have a list of 68 possible pairs for two words, we're going to want to start there when we add in a third word, rather than testing all 8 x 409 x 48 = 157,056 triples as the function currently does. I leave these improvements as an exercise for the reader.

Attachments:

PatternWords.nb