Group Abstract Group Abstract

Message Boards Message Boards

Play with Music Scales Samples

I thought it would be interesting make a simple post about the several musical scales and Mathematica.

I know there are many and very good posts on this topic, about timing, chord and music construction, that´s not what I approach here. I just wanted to do one post on a simple form about the different scales, so that a person not so experienced could enjoy. Here is shown in a very simple way the relationship between the musical notes in various scales and tones, frequency of the notes in hertz and the many sonorities. Samples of the scales with various instruments, only for fun and knowledge.

Below are the 30 musical scales that I address in this post:

i1

As already explained in the Documentation, the note chosen by convention to be the integer frequency is the A of 440 hertz, from which all other notes are calculated:

440*(2^(n/12) // DisplayForm)

i2

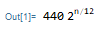
Example of other note frequencies:

Do[Print@N[440*2^(n/12)], {n, -5, 5}]

i3

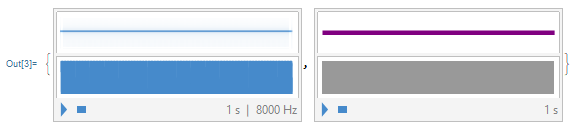
This conventional A note is similar to the numerical value “9” in coding by Mathematica. Below is the A 440 hertz generated by both the frequency and the numerical value stipulated by the program. In this example the duration is 1 second:

{Play[Sin[2*Pi*440*t], {t, 0, 1}], Sound@SoundNote[9, 1]}

i4

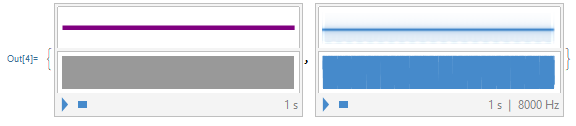
Mathematica uses as the base value the middle C note (C4, or C of the fourth octave ) which is represented by the numerical value “0” in the program. This value is 9 semi-tones (or 9 numeric values) below A 440 hertz and has a frequency of approximately 261,626 hertz. Below is this middle C generated both by the default value 0 of Mathematica and by the value generated using the frequency:

{Sound@SoundNote[0, 1], Play[Sin[2*Pi*440*2^(-3/4)*t], {t, 0, 1}]}

i5

An example of how to find the numeric notes and their respective frequency by equation:

Do[Print[{n, N[440*2^((n - 9)/12)]}], {n, -10, 10}]

i6

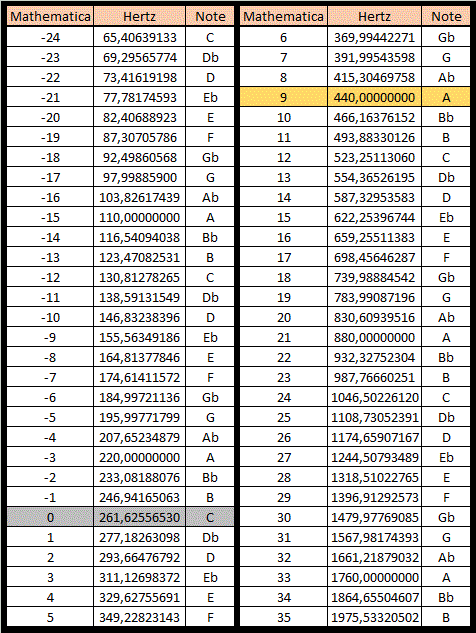
Here is a brief summary of the notes in Mathematica, their frequencies and their tones:

i7

Since in this post I show several musical scales which have different tones ( Gb, F, G, Ab... ), it is interesting to know how to make the change of tones. Below is an example of how to change tones in any scale shown here. For example, if we take the major pentatonic in Gb and want it in A, we need to add 3 in the numerical value of all the scale notes: Gb (-18 for example) to A (-15 for example) we need to add 3. Below is a tone conversion for this example scale:

MajorPentatonicGb = {-18, -16, -14, -11, -9, -6, -4, -2, 1, 3, 6, 8};
MajorPentatonicA = 3 + MajorPentatonicGb
MajorPentatonicA /. {-20 -> "E", -19 -> "F", -18 -> "Gb", -17 -> 
   "G", -16 -> "Ab", -15 -> "A", -14 -> "Bb", -13 -> "B", -12 -> 
   "C", -11 -> "Db", -10 -> "D", -9 -> "Eb", -8 -> "E", -7 -> 
   "F", -6 -> "Gb", -5 -> "G", -4 -> "Ab", -3 -> "A", -2 -> 
   "Bb", -1 -> "B", 0 -> "C", 1 -> "Db", 2 -> "D", 3 -> "Eb", 
  4 -> "E", 5 -> "F", 6 -> "Gb", 7 -> "G", 8 -> "Ab", 9 -> "A", 
  10 -> "Bb", 11 -> "B", 12 -> "C"}

i8

Here is a simple function for listening to the sound of the different scales ( in a gentler way, not too complicated ) and the numerical sequence code of the scales. Then the instruments used are varied only for better contemplation as well as intervals of notes, but any of the scales may have other intervals and instrumentation:

mf[a_, b_, c_] := Module[{n},
  n = Take[Flatten@RandomSample@Join[Subsets[a, {3, 7}],
       Map[Sort[#, Greater] &, Subsets[a, {3, 7}]],
       Map[RandomSample, Subsets[a, {2, 5}]]], 1000]; 
  Sound@Map[SoundNote[#, (1 + RandomReal[{-0.1, 0.1}])*b, c] &, n]]

MajorPentatonic = {-18, -16, -14, -11, -9, -6, -4, -2, 1, 3, 6, 8};
MinorPentatonic = {-19, -16, -14, -12, -9, -7, -4, -2, 0, 3, 5, 8};
NeopolitanMajor = {-19, -18, -17, -15, -13, -11, -9, -7, -6, -5, -3, \
-1, 1, 3, 5, 6, 7, 9};
NeopolitanMinor = {-18, -17, -15, -13, -11, -10, -7, -6, -5, -3, -1, 
   1, 2, 5, 6, 7, 9};
HungarianMajor = {-18, -15, -14, -12, -11, -9, -8, -6, -3, -2, 0, 1, 
   3, 4, 6, 9};
HungarianMinor = {-19, -18, -16, -15, -12, -11, -10, -7, -6, -4, -3, 
   0, 1, 2, 5, 6, 8, 9};
HungarianGypsy = {-19, -17, -15, -13, -11, -10, -9, -7, -5, -3, -1, 1,
    2, 3, 5, 7, 9};
HarmonicMajor = {-19, -18, -16, -14, -13, -11, -10, -7, -6, -4, -2, \
-1, 1, 2, 5, 6, 8};
HarmonicMinor = {-19, -18, -16, -15, -13, -11, -10, -7, -6, -4, -3, \
-1, 1, 2, 5, 6, 8, 9};
DoubleHarmonic = {-17, -16, -15, -12, -11, -9, -8, -5, -4, -3, 0, 1, 
   3, 4, 7, 8, 9};
JazzMinor = {-19, -18, -16, -15, -13, -11, -9, -7, -6, -4, -3, -1, 1, 
   3, 5, 6, 8, 9};
Overtone = {-19, -17, -15, -13, -11, -10, -8, -7, -5, -3, -1, 1, 2, 4,
    5, 7, 9};
BluesScale = {-19, -16, -14, -13, -12, -9, -7, -4, -2, -1, 0, 3, 5, 8};
Chromatic = {-15, -14, -13, -12, -11, -10, -9, -8, -7, -6, -5, -4, \
-3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
WholeTone = {-19, -17, -15, -13, -11, -9, -7, -5, -3, -1, 1, 3, 5, 7, 
   9, 11, 13, 15};
DiminishedWholeTone = {-18, -17, -15, -14, -12, -10, -8, -6, -5, -3, \
-2, 0, 2, 4, 6, 7, 9};
Symmetrical = {-19, -17, -16, -14, -13, -11, -10, -8, -7, -5, -4, -2, \
-1, 1, 2, 4, 5, 7, 8};
Arabian = {-19, -17, -15, -13, -12, -11, -9, -7, -5, -3, -1, 0, 1, 3, 
   5, 7, 9};
Balinese = {-19, -18, -16, -12, -11, -7, -6, -4, 0, 1, 5, 6, 8};
Byzantine = {-19, -18, -17, -14, -13, -11, -10, -7, -6, -5, -2, -1, 1,
    2, 5, 6, 7};
Persian = {-19, -18, -17, -14, -13, -12, -10, -7, -6, -5 - 2, -1, 0, 
   2, 5, 6, 7, 10};
EastIndianPurvi = {-19, -18, -17, -14, -12, -11, -10, -7, -6, -5, -2, 
   0, 1, 2, 5, 6, 7};
Oriental = {-19, -18, -16, -15, -12, -11, -10, -7, -6, -4, -3, 0, 1, 
   2, 5, 6, 8, 9};
GagakuRyoSenPou = {-18, -16, -14, -11, -9, -6, -4, -2, 1, 3, 6, 8};
Zokugaku = {-19, -16, -14, -12, -9, -7, -4, -2, 0, 3, 5, 8};
InSenPou = {-19, -18, -14, -12, -11, -7, -6, -2, 0, 1, 5, 6};
Okinawa = {-19, -18, -14, -13, -11, -7, -6, -2, -1, 1, 5, 6};
Enigmatic = {-19, -18, -17, -14, -12, -10, -8, -7, -6, -5, -2, 0, 2, 
   4, 5, 6, 7, 10};
EightToneSpanish = {-18, -16, -15, -13, -12, -11, -10, -8, -6, -4, \
-3, -1, 0, 1, 2, 4, 6, 8, 9};
Prometheus = {-18, -16, -14, -12, -9, -8, -6, -4, -2, 0, 3, 4, 6, 8};

Below are the examples of the scales that can be played by the musical function shown above:

  • Major Pentatonic:

Has 5 scale notes. The image below is an exemplificative tone C and the scale sample is in Gb tone: { Gb, Ab, Bb, Db, Eb }.

i9

mf[MajorPentatonic, 0.22, "Guitar"]
  • Minor Pentatonic:

Has 5 scale notes. The image below is an exemplificative tone C and the scale sample is in F tone: { F, Ab, Bb, C, Eb }.

i10

mf[MinorPentatonic, 0.22, "Guitar"]
  • Neopolitan Major:

Has 7 scale notes. The image below is an exemplificative tone C and the scale sample is in Gb tone: { Gb, G, A, B, Db, Eb, F }.

i11

mf[NeopolitanMajor, 0.22, "ElectricBass"]
  • Neopolitan Minor:

Has 7 scale notes. The image below is an exemplificative tone C and the scale sample is in Gb tone: { Gb, G, A, B, Db, D, F }.

i12

mf[NeopolitanMinor, 0.22, "ElectricBass"]
  • Hungarian Major:

Has 7 scale notes. The image below is an exemplificative tone C and the scale sample is in Gb tone: { Gb, A, Bb, C, Db, Eb, E }.

i13

mf[HungarianMajor, 0.23, "SteelGuitar"]
  • Hungarian Minor:

Has 7 scale notes. The image below is an exemplificative tone C and the scale sample is in Gb tone: { Gb, Ab, A, C, Db, D, F }.

i14

mf[HungarianMinor, 0.23, "SteelGuitar"]
  • Hungarian Gypsy:

Has 7 scale notes. The image below is an exemplificative tone C and the scale sample is in G tone: { G, A, B, Db, D, Eb, F }.

i15

mf[HungarianGypsy, 0.18, "Glockenspiel"]
  • Harmonic Major:

Has 7 scale notes. The image below is an exemplificative tone C and the scale sample is in Gb tone: { Gb, Ab, Bb, B, Db, D, F }.

i16

mf[HarmonicMajor, 0.2, "ElectricGrandPiano"]
  • Harmonic Minor:

Has 7 scale notes. The image below is an exemplificative tone C and the scale sample is in Gb tone: { Gb, Ab, A, B, Db, D, F }.

i17

mf[HarmonicMinor, 0.2, "Piano"]
  • Double Harmonic:

Has 7 scale notes. The image below is an exemplificative tone C and the scale sample is in Ab tone: { Ab, A, C, Db, Eb, E, G }.

i18

mf[DoubleHarmonic, 0.15, "Guitar"]
  • Jazz Minor:

Has 7 scale notes. The image below is an exemplificative tone C and the scale sample is in Gb tone: { Gb, Ab, A, B, Db, Eb, F }.

i19

mf[JazzMinor, 0.18, "GuitarHarmonics"]
  • Overtone:

Has 7 scale notes. The image below is an exemplificative tone C and the scale sample is in G tone: { G, A, B, Db, D, E, F }.

i20

mf[Overtone, 0.22, "Crystal"]
  • Blues Scale:

Has 6 scale notes. The image below is an exemplificative tone C and the scale sample is in F tone: { F, Ab, Bb, B, C, Eb }.

i21

mf[BluesScale, 0.33, "ElectricPiano"]
  • Chromatic:

Has 12 scale notes. The image below is an exemplificative tone C and the scale sample is in A tone: { A, Bb, B, C, Db, D, Eb, E, F, Gb, G, Ab }.

i22

mf[Chromatic, 0.17, "PanFlute"]
  • Whole Tone:

Has 6 scale notes. The image below is an exemplificative tone C and the scale sample is in F tone: { F, G, A, B, Db, Eb }.

i23

mf[WholeTone, 0.2, "PizzicatoStrings"]
  • Diminished Whole Tone:

Has 7 scale notes. The image below is an exemplificative tone C and the scale sample is in Gb tone: { Gb, G, A, Bb, C, D, E }.

i24

mf[DiminishedWholeTone, 0.24, "ElectricBass"]
  • Symmetrical:

Has 8 scale notes. The image below is an exemplificative tone C and the scale sample is in G tone: { G, Ab, Bb, B, Db, D, E, F }.

i25

mf[Symmetrical, 0.17, "Guitar"]
  • Arabian:

Has 7 scale notes. The image below is an exemplificative tone C and the scale sample is in G tone: { G, A, B, C, Db, Eb, F }.

i26

mf[Arabian, 0.3, "Cello"]
  • Balinese:

Has 5 scale notes. The image below is an exemplificative tone C and the scale sample is in F tone: { F, Gb, Ab, C, Db }.

i27

mf[Balinese, 0.31, "Banjo"]
  • Byzantine:

Has 7 scale notes. The image below is an exemplificative tone C and the scale sample is in Gb tone: { Gb, G, Bb, B, Db, D, F }.

i28

mf[Byzantine, 0.23, "Bandoneon"]
  • Persian:

Has 7 scale notes. The image below is an exemplificative tone C and the scale sample is in Gb tone: { Gb, G, Bb, B, C, D, F }.

i29

mf[Persian, 0.3, "Tuba"]
  • East Indian Purvi:

Has 7 scale notes. The image below is an exemplificative tone C and the scale sample is in Gb tone: { Gb, G, Bb, C, Db, D, F }.

i30

mf[EastIndianPurvi, 0.25, "Sitar"]
  • Oriental:

Has 7 scale notes. The image below is an exemplificative tone C and the scale sample is in Ab tone: { Ab, A, C, Db, D, F, Gb }.

i31

mf[Oriental, 0.3, "GuitarMuted"]
  • Gagaku Ryo Sen Pou:

Has 5 scale notes. The image below is an exemplificative tone C and the scale sample is in Gb tone: { Gb, Ab, Bb, Db, Eb }.

i32

mf[GagakuRyoSenPou, 0.2, "Harp"]
  • Zokugaku:

Has 5 scale notes. The image below is an exemplificative tone C and the scale sample is in F tone: { F, Ab, Bb, C, Eb }.

i33

mf[Zokugaku, 0.32, "Shamisen"]
  • In Sen Pou:

Has 5 scale notes. The image below is an exemplificative tone C and the scale sample is in F tone: { F, Gb, Bb, C, Db }.

i34

mf[InSenPou, 0.28, "Guitar"]
  • Okinawa:

Has 5 scale notes. The image below is an exemplificative tone C and the scale sample is in Gb tone: { Gb, Bb, B, Db, F }.

i35

mf[Okinawa, 0.42, "Agogo"]
  • Enigmatic:

Has 7 scale notes. The image below is an exemplificative tone C and the scale sample is in Gb tone: { Gb, G, Bb, C, D, E, F }.

i36

mf[Enigmatic, 0.2, "ElectricPiano2"]
  • Eight Tone Spanish:

Has 8 scale notes. The image below is an exemplificative tone C and the scale sample is in Ab tone: { Ab, A, B, C, Db, D, E, Gb }.

i37

mf[EightToneSpanish, 0.18, "Crystal"]
  • Prometheus:

Has 6 scale notes. The image below is an exemplificative tone C and the scale sample is in Gb tone: { Gb, Ab, Bb, C, Eb, E }.

i38

mf[Prometheus, 0.28, "Organ"]

The images with the scales above came from the Mel Bay's Complete Guitar Scale Dictionary, by Mike Christiansen.

I hope this post is useful to someone in the community, or someone who just likes to appreciate the different sounds of the scales.

Thank you very much.
POSTED BY: Claudio Chaib
2 Replies
Sort By:
POSTED BY: Claudio Chaib
POSTED BY: Daniel Lichtblau
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard