Dear Mathematica team:
I am trying witout success to make a change of variables in a partial derivative of a function of 2 variables (for example the time coordinate "t" and the lenght coordinate "z"), like
fu:= f[t,z]
dfu:= D[fu,{{t,z}}]
Then I want to rescale the t and z coordinates (something that is useful for example to simplify equations in fluid mechanics), defining the new variables: z0=z/L; t0= t*u/L
z0:=z/L
t0:= t*u/L
Putting all together:
{t0,z0}:={t*u/L,z/L}
fu:= f[t0,z0]
dfu:= D[fu,{{t0,z0}}]
Unfortunately, this substitution does not work because I am actually differentiating with respect to functions of the original t and z variables, so the program send and error message like: "z/L is not a valid variable"
After some reading of calculus textbooks, I found that I need to apply the chain rule. The problem with this is twofold:
1) The formulae are a bit messy, like these in the Wilfred Kaplan (2002) textbook: 
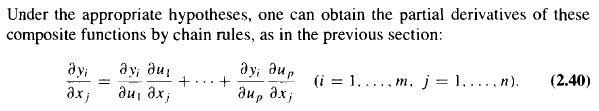

Those formulae have either explicit sums or products of Jacobian matrices, and while constructing Jacobians from substitution rules (like the reascaling ones above) is rather easy, I still don't undestand how to implement the full formulae in Mathematica.
I would greatly appreciate you help.
Nota bene: maybe someone else posted something similar before (my apologies if it is the case) , I just don't know yet how to seach by keywords in the forum.