The summer school project is a first step towards developing the application of the tools of nonlinear dynamics to measuring rocks, to measuring the structural architectures which result from processes interacting and developing in a coupled environment.

I am concerned with the processes that operate during the deformation and metamorphism of rocks in the crust and upper lithosphere of the Earth. The deformation and metamorphism of rocks involves structural rearrangements of elements of the rock at the microscale by processes such as mass diffusion, dislocation slip and climb, grain-boundary migration and fracturing at the same time as chemical reactions proceed. In some instances infiltrating fluids introduce or remove chemical components and may influence mechanical properties through changes in mineralogical composition, fluid pressure or temperature. At the same time, heat is added to or removed from the system depending on the surrounding tectonic environment. Such mechanisms do not operate independently of each other but are coupled so that each process has feedback influences on the others leading to structures and mineral assemblages that do not develop in the uncoupled environment.

Some aspects of this research are represented by this Word Cloud:

The characterisation of nonlinear systems in terms of multifractal geometry and recurrence in the dynamics constitutes an important tool box for geological systems.

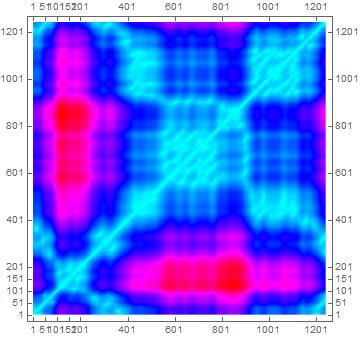
An important concept in nonlinear analysis is the recurrence plot; this contains all the information that defines the underlying dynamics of a system. A recurrence plot determines the times (or locations for a spatially patterned signal) at which a trajectory in phase space visits roughly the same area in that phase space. Distances are measured in the embedding space of the attractor for the system. The complete dynamics of a system can be derived from a time (or spatial) series for a single state variable from that system (Takens) so that the dynamics of the system are encompassed by the attractor for that system. The input data are not constrained to any type of statistical distribution and the data are not required to be stationary. There is no need to know the mathematical rules (if any) governing the system under study.

Quantification of a recurrence plot such as that shown here has been developed by Webber and Marwan (2015).

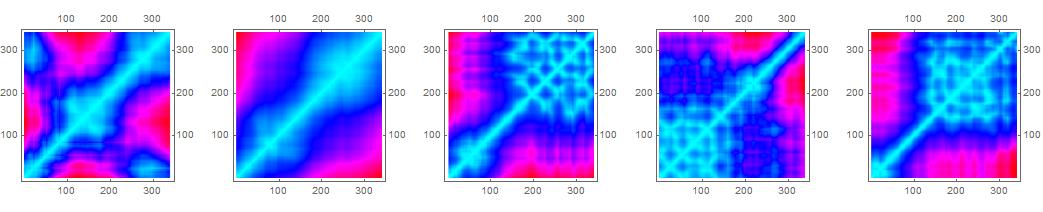
Further details of the multiscaling of the system may be explored through windows moving along the main diagonal. The structures in the five windows shown here may be matched with their position in the main window.

Prediction based on nonlinear dynamics, in this case through recurrence quantification analysis, takes into account the full mechanics of the formation of the geological system.

The Wolfram Language Notebook containing the details of the analysis performed at the Wolfram Summer School 2019 is available here.