Introduction
A Petri net includes places, transitions and arcs. Arcs must go from a place to a transition or vice versa, which makes a Petri net a directed bipartite graph and the nodes represent transitions (events that may occur to cause change in states, marked by square) and places (conditions, marked by circles). These conditions make our first group of functions to check if the input structure is a Petri net, with the function named petriNetQ. Petri net is very useful because it is inherently graphical, good at representing concurrency and some interesting properties of nets can be expressed in terms of reachability. Hope more can be added to make the Petri net package more powerful.
Visualization and Animation
Here we have a package to make a Petri net and visualize it.
ClearAll[petriNetRun];
petriNetRun[pnet_, init_, step_Integer]:= Module[
{current = init, g, index},
current = Nest[updateFiring[pnet], current, step-1];
index = First @ RandomChoice[Position[checkFiring[pnet, #, current] &/@ pnet[[3]], True]];
If[IntegerQ[index],
makeFiring[pnet, pnet[[3,index]], current],
Print["Dead!"]; Abort[]];
g = petriNetInit[pnet, current];
HighlightGraph[g, {pnet[[3,index]]}]
]
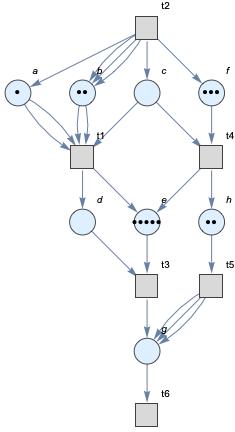
We then tried to visualize the movement of the Petri net in 15 steps.
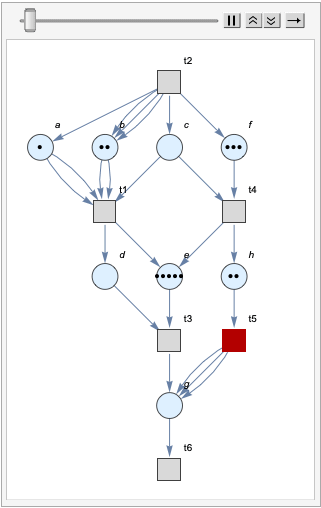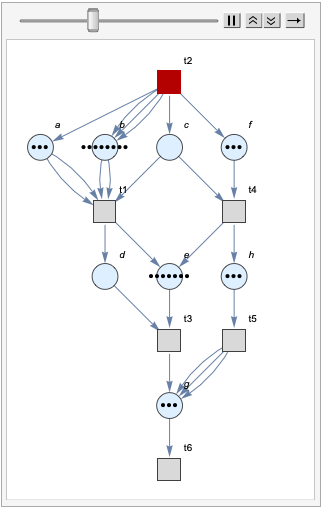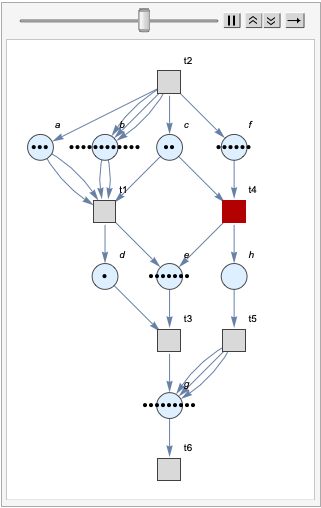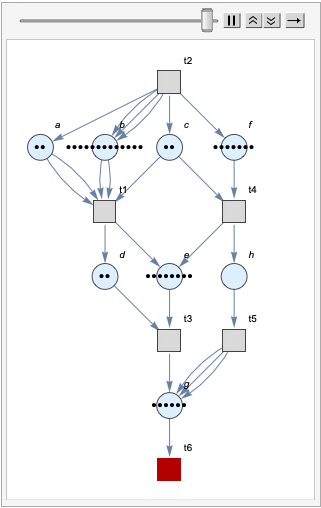
Also for convenience, we have three different user interface to generate Petri net given Petri net data structure, chemical reactions and system of transitions.
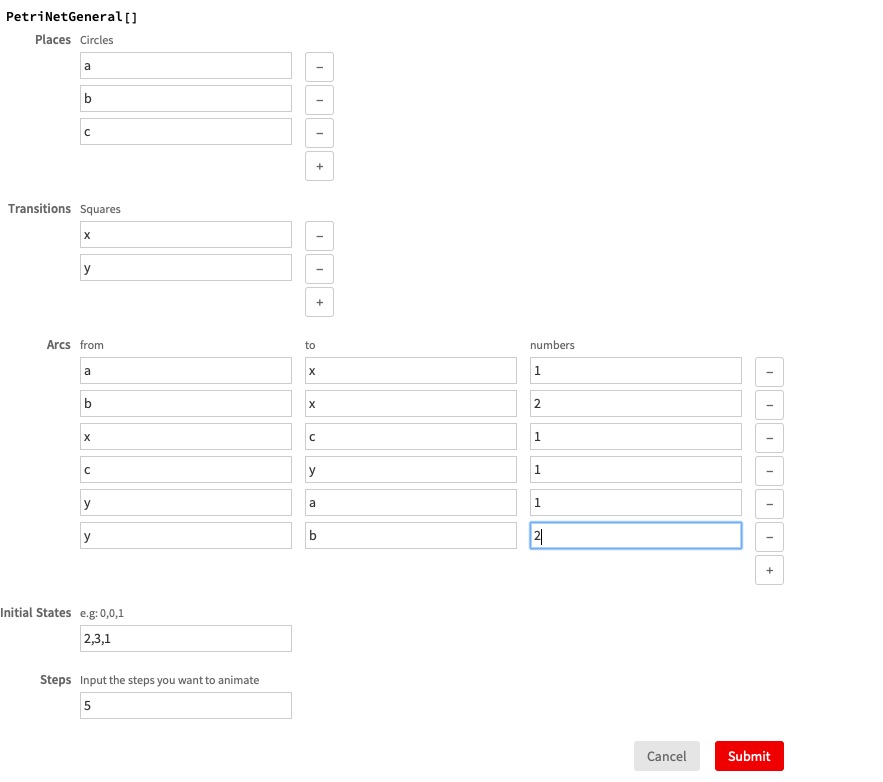
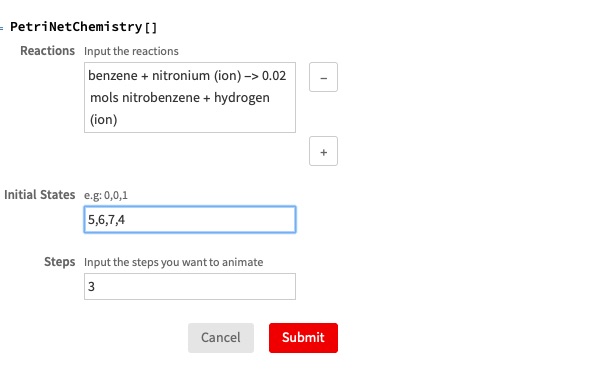
If a user gives the correct input, he or she will receive an animation of the Petri net similar to the one we display.
Petri net properties
Petri net, as a mathematical modeling language, indeed is not limited to visualize chemical processes. In fact, any mathematics model can be somewhat expressed with Petri net. However, from Wikipedia, papers written by John Baez, and StateBox archive, here are some open questions discussed with Petri net. The first problem is Reachability. According to Wikipedia, The reachability problem for Petri nets is to decide, given a Petri net N and a marking M, whether M can be reached from current state. This problem actually is not easy, and it was shown to be EXPSPACE-hard. But these days it turned out to be elementary. Here is a function named petriNetReachableQ.
petriNetReachableQ [ Neural Net n, init, Node m ]
Input: A Petri net named n, the initial condition of states, and the node marked as m we want to check.
Return: True if for Net n, m is reachable given the initial condition init in finite steps, else return False.
ClearAll[petriNetReachableQ];
petriNetReachableQ[pnet_, init_, place_]:= Module[
{states, places, assoc},
states = Total[NestList[updateFiring[pnet], init , 100]];
places = First @ Rest @ pnet;
assoc = Association[Thread[places -> states]];
If[assoc[place] === 0, False, True]
]
An example to run petriNetReachableQ is the following:
In[61]:= petriNetReachableQ[graph, {1, 2, 0, 0, 5, 3, 0, 2}, c]
Out[61]= True
There are other properties remain discussed, such as boundedness and liveness. These are interesting graph properties we want to discuss here in Petri net. For a place p in a Petri Net, it is k-bounded if it never contains more than k tokens in any reachable marking. For example, traffic light nets are bounded, since every places are 1-bounded, which means the system is in safe.
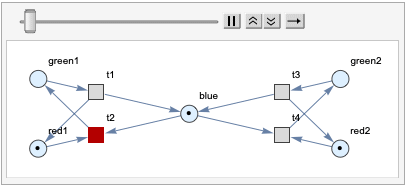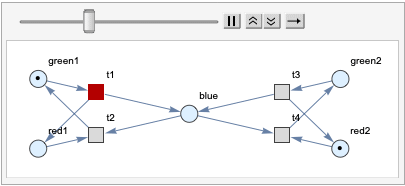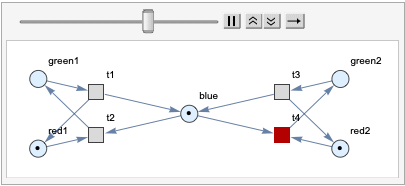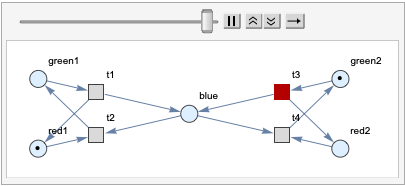
kBoundedness[Petri net pnet, initial state, key p]:
Input: Petri net named pnet, initial state of the Petri net pnet and the state key we what to check.
Return: an integer shows the boundedness of the state key.
For example, we want to check the boundedness of the red light from the Petri net we created, which is 1.
In[63]:= kBoundedness[graph, {1, 0, 1, 0, 1}][red1]
Out[63]= 1
 Attachments:
Attachments: