 Abstract
Abstract
In order to automatically grade student problems, one must identify the scope and level of the problem and then define equivalent answers appropriate to the context of the question and knowledge of the student. To this end, we first train a Neural Network Classifier on a data set of problems in Algebra 1, Algebra 2 and Calculus. Then, using a combination of rule-based checks and the theorem prover, we define equivalent answers, then check that particular rules were not used in order to maintain equivalence at the level of the student to prevent cheating.
Introduction
When providing questions to students online, the teacher is often left with a dilemma. Do you give the student a multiple choice problem that fails to properly test their ability by allowing guessing, or do you give them a long answer that will only accept one correct answer, when there might be multiple equivalent answers? To add in all possible answers would be an onerous task, thus it would be preferable to have the system automatically identify all possible answers. However, this presents a challenge in its own right. How does one limit the possible answers to those that the student would have reached based on the level of their knowledge, and how does one deal with problems that may limit the scope of the equivalent answers? To this end, we define a two-part problem: classification of the problem's level and scope and cross-checking for equivalent answers.
Classification and context identification
The problem of classification is often solved by machine learning techniques trained on large data sets. In this case, I retrained a series of models in the Wolfram language "Classify" function on an 1800 question data set in algebra 1, 2 and calculus, grouping all the problems and providing the problems and groupings to the network, i.e. training in a supervised manner. Then, the accuracy of each model was tested by comparing the probability of identification as the proper grouping to the highest probability of the other two groups, using:
Clear[questionClassifier]
questionClassifier =
Classify[<|"algebra 1" -> algebra1Questions,
"algebra 2" -> algebra2Qs|> , PerformanceGoal -> "Quality",
Method -> "Markov"]
algebra1IsAlgebra1 =
questionClassifier[algebra1Questions, {"Probability", "algebra 1"}];
algebra1IsAlgebra2 =
questionClassifier[algebra1Questions, {"Probability", "algebra 2"}];
algebra2IsAlgebra1 =
questionClassifier[algebra2Qs, {"Probability", "algebra 1"}];
algebra2IsAlgebra2 =
questionClassifier[algebra2Qs, {"Probability", "algebra 2"}];
lp = ListLogPlot[#right/#wrong &@ <|"right" -> algebra1IsAlgebra1,
"wrong" -> algebra1IsAlgebra2|>, AxesLabel -> {"Data"},
PlotLabel -> "Algebra 1 ", GridLines -> {{}, {1}},
GridLinesStyle -> Red] ;
lp1 = ListLogPlot[#right/#wrong &@ <|"right" -> algebra2IsAlgebra2,
"wrong" -> algebra2IsAlgebra1|>, AxesLabel -> {"Data"},
PlotLabel -> "Algebra 2", GridLines -> {{}, {1}},
GridLinesStyle -> Red];
Where the data sets are drawn from "finalprojecttrainingdata.mx" (attached).
All models were given the "Quality" goal to improve accuracy at the cost of training time, as the training is taking place ahead of time, and the system is not retrained live. However, when this was performed on data generated by the Wolfram|Alpha Problem Generator, where the addition of calculus made "What is 1+1" evaluate as calculus independent of the number of inputs. Thus, the calculus tag was removed, and this identification was moved to a context-based pattern matching. Total training inputs are 1302, with 651 each of algebra 1 and 2. 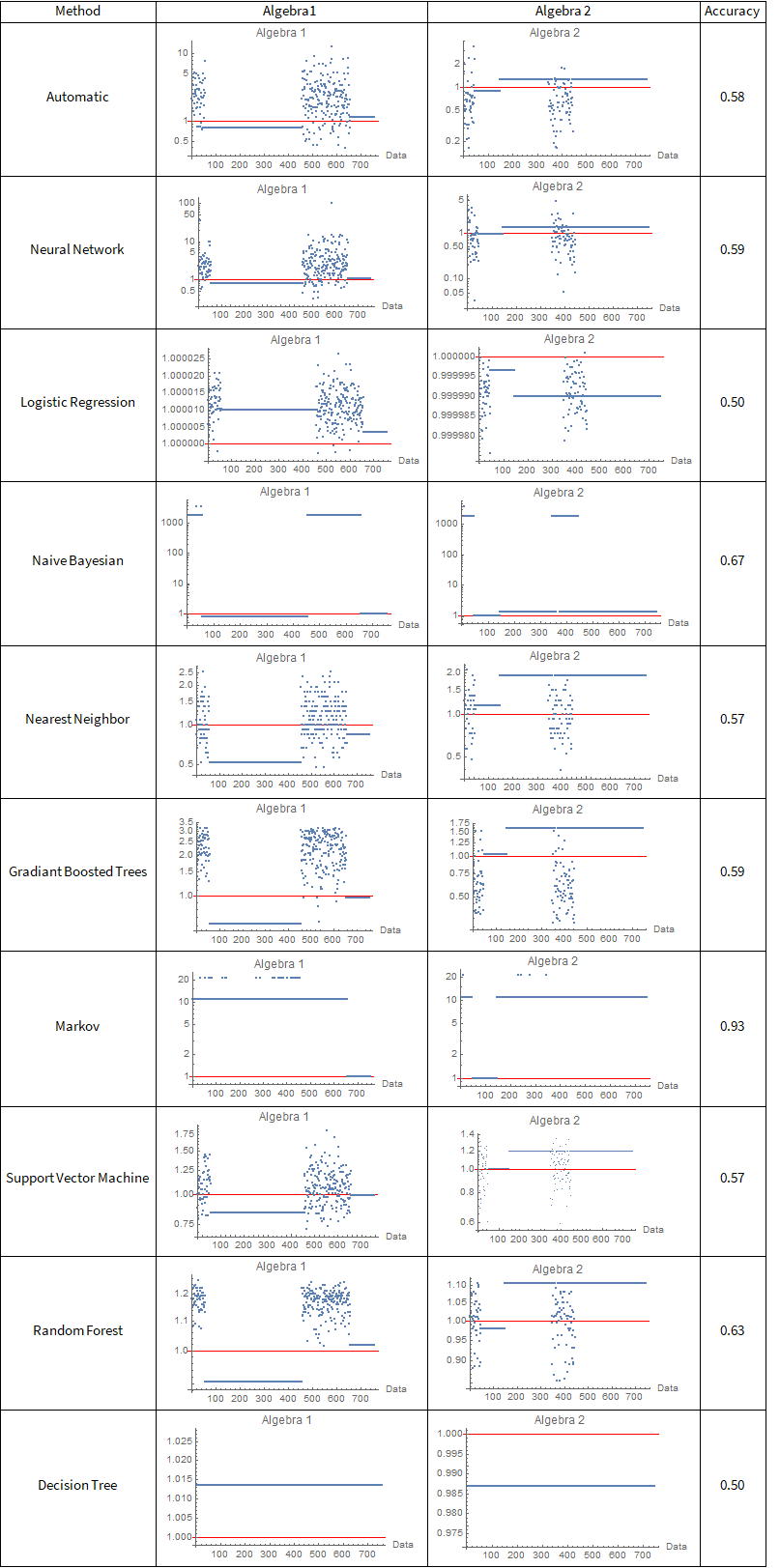
From the above results, one can clearly see that the Markov model is superior on this data set, however, it may be worse for others.
Identification of Context
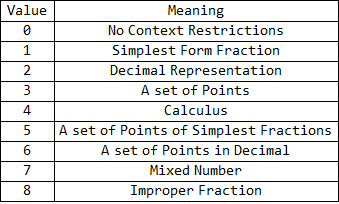
The context of the problem, however, does not get captured by the classifier above. The classifier simply finds the level, meanwhile the context, for example, would be "write your answer as a simplified fraction". These contexts are identified via pattern matching. These rules are then used to assign a specific tag:
turnOffEquivFrac[question_] :=
StringMatchQ[question, {"*raction*implest form"}];
isMatrixQ[answer_] := MatchQ[answer, MatrixForm];
allpoints[question_] := StringMatchQ[question, {"*all points*"}];
eitherPointfirst[a_, b_, c_,
d_] := {{"(", a, b, ")"}, {"(" c, d ")"}} -> {{"(" c, d ")"}, {"(",
a, b, ")"}}
isPoint[answer_] := StringMatchQ[answer, {"(*,*)"}];
improperFraction[question_] :=
StringMatchQ[question, "*mproper fraction*"];
decForm[question_] := StringMatchQ[question, "*ecimal form*"];
isCalcQ[question_] :=
StringMatchQ[
question, {"*erivative*", "*ifferniate*", "*ntegra*",
"*aylor*xpand*", "*acLa*xpand*", "*imit*"}];
mixedNumber[question_] := StringMatchQ[question, "*ixed number*"];
Identifying Correct Answers
The identification of correct answers was performed by the implementation of the below code as part of a new package.
correctAnswer[answer_, correct_]:=MatchQ[Interpreter["MathExpression"][answer], Interpreter["MathExpression"][correct]]
turnOffEquivFrac[question_]:=StringMatchQ[question, {"*raction*implest form"}];
isMatrix[answer_]:=MatchQ[answer, MatrixForm];
allpoints[question_]:=StringMatchQ[question, {"*all points*"}];
eitherPointfirst[a_, b_,c_, d_]:= {{"(",a, b, ")"},{"("c, d ")"}}-> {{"("c, d ")"},{"(",a, b, ")"}}
isPoint[answer_]:=StringMatchQ[answer, {"(*,*)"}];
improperFraction[question_]:=StringMatchQ[question, "*mproper fraction*"];
decForm[question_]:=StringMatchQ[question, "*ecimal form*"];
isCalc[question_]:=StringMatchQ[question, {"*erivative*", "*ifferniate*", "*ntegra*", "*aylor*xpand*", "*acLa*xpand*", "*imit*"}];
mixedNumber[question_]:=StringMatchQ[question, "*ixed number*"];
(*This is the wrong way to do it, patern matching is better here*)
expandToSix[answer_, correct_, x_]:=If[Series[answer, {x, 0, 6}]==Series[correct, {x, 0, 6}], True, False]
algebratheorems={ForAll[{a,b,c}, g[a, g[b,c]]==g[g[a, b], c]],
ForAll[{a,b}, g[a, b]==g[b,a]],
ForAll[{a,b}, f[a,b]==f[b,a]],
ForAll[{a,b,c}, f[a,f[b,c]]==f[f[a,b],c]],
ForAll[{a,b,c}, f[a, g[c,b]]==g[f[a,c], f[a,b]]],
ForAll[a, g[a,e]==a],
ForAll[a, f[a, e]==e],
ForAll[a, f[a, n]==a],
ForAll[a, g[a, inv[a]]==e],
ForAll[a, f[a, inv1[a]]==n]} (*This defines an abelian ring w/ distributive property*)
algebraandtrigtheorems={ForAll[{a,b,c}, g[a, g[b,c]]==g[g[a, b], c]],
ForAll[{a,b}, g[a, b]==g[b,a]],
ForAll[{a,b}, f[a,b]==f[b,a]],
ForAll[{a,b,c}, f[a,f[b,c]]==f[f[a,b],c]],
ForAll[{a,b,c}, f[a, g[c,b]]==g[f[a,c], f[a,b]]],
ForAll[a, g[a,e]==a],
ForAll[a, f[a, e]==e],
ForAll[a, f[a, n]==a],
ForAll[a, g[a, inv[a]]==e],
ForAll[a, f[a, inv1[a]]==n],
ForAll[{a,b}, sin[g[a,b]]==g[f[sin[a],cos[b]], f[sin[b], cos[a]]]],
ForAll[ {a,b}, cos[g[a,b]]==g[f[cos[a],cos[b]], f[sin[inv[b]], sin[a]]]],
ForAll[a, sin[inv[a]]==inv[sin[a]]],
ForAll[a, cos[inv[a]]==cos[a]],
ForAll[a, g[f[sin[a],sin[a]], f[cos[a], cos[a]]]==n]}
theorems=<|"algebra 1"-> {algebratheorems}, "algebra 2"-> {algebraandtrigtheorems}, "calc"-> {algebraandtrigtheorems}|>;
removeSinCos[given_]:=given/.{Sin->sin, Cos->cos}
removeSinCos[Sin[5]+Cos[x]]
replacePlus[given_]:=given/.{Plus-> g, Times[-1, amin_]->inv[amin]}
replacePlus[a-b]
replaceMulti[given_]:=given/.{Times-> f, Power[adiv_, -1]-> inv1[adiv]}
replaceTanSecCscCot[given_]:=given/.{Tan[atan_]-> f[sin[atan],inv1[cos[atan]]], Sec[asec_]-> inv1[cos[asec]], Csc[acsc_]-> inv1[sin[acsc]], Cot[acot_]-> f[inv1[sin[acot]],cos[acot]]}
replaceTanSecCscCot[Tan[y]+ Csc[x]]
removeProperFormat[given_]:=replacePlus[replaceMulti[removeSinCos[replaceTanSecCscCot[given]]]]
determinetags[question_]:=If[allpoints[question],
If[turnOffEquivFrac[question], 5,
If[decForm[question], 6, 3]],
If[turnOffEquivFrac[question], 1,
If[decForm[question], 2,
If[isCalc[question], 4,
If[mixedNumber[question], 7,
If[improperFraction[question], 8, 0]
]
]
]
]
];
equivalentAnswer[level_, tags_, answer_, correct_]:=
Module[{formattedanswer, formattedcorrectanswer, proof},
If[tags==4, level="calc"];
Switch[tags,
0| 3| 4, If[correctAnswer[answer, correct], True, If[Simplify[Interpreter["MathExpression"][answer]- Interpreter["MathExpression"][correct]]==0,
If[UnsameQ[Head[Interpreter["MathExpression"][answer]], Failure],
formattedanswer:=removeProperFormat[Interpreter["MathExpression"][answer]];
formattedcorrectanswer=removeProperFormat[Interpreter["MathExpression"][correct]];
proof=TimeConstrained[FindEquationalProof[formattedanswer==formattedcorrectanswer , theorems[level]],10];
If[proof["Logic"]=="EquationalLogic",
If[Complement[Query[Key[{"SubstitutionLemma", All}proof["ProofDataset"]["Statement"]]], theorems[level]]=={}, True, False],
False],
False],
False]],
1, If[correctAnswer[answer, correct], True, False],
2, If[correctAnswer[answer, correct], True, False],
5, If[Complement[StringSplit[answer, "),("], StringSplit[correct, "),("]]=={}, True, False],
6, If[Complement[StringSplit[answer, "),("], StringSplit[correct, "),("]]=={}, True, False],
_, MatchQ[answer, correct] (*exact match is default case*)
]]
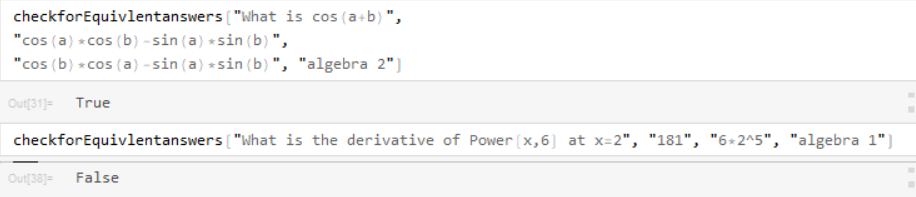
checkforEquivlentanswers[question_, answer_, correct_, level_]:=
Module[{t},
t=determinetags[question];
equivalentAnswer[level, t, answer, correct]]
Conclusions and Future Work
This project has developed a Classifier and a Package that may be implemented in a variety of applications. Ideally, one can consider two exemplars. One has the student submits an answer to a randomly selected question from a database that has been built using Wolfram|Alpha's Problem Generator. The student may select one of the three levels, receive a question, submit an answer and check that it is correct. After the correct answer has been submitted, the system automatically pulls a new question from the list in the selected type. The second allows for the teacher to create a quiz and store it as a new database, which will then be fed to the first exemplar. Thus, we see this project as a quiet server-side application, and as a service that would be deliverable to a client. Further work could encompass the addition of further levels of questions, the use of graphical data as a selected answer or the inclusion of a retraining function in the neural net to improve classification accuracy, as well as the integration of the data into the described GUIs.
 Attachments:
Attachments: