Introduction

The task of finding the minimum change path between Wolfram Language expressions is very similar to the tree-to-tree correction problem, with an algorithm for the most general case developed by K-C Tai in 1979, and later subject to various optimisations by K.Zhang and D.Shahsa in 1989 and E.D. Demaine et al. in 2009. This problem considers rooted, ordered and labelled trees and the minimum number of edit operations we must perform to transform between them. The edit operations are limited to replacements, deletions and insertions. Using the tree form of Wolfram Language expressions as an analogue to rooted, ordered and labelled trees, we define the notion of distance between Wolfram Language expressions and implement a way to search for and perform the sequence of minimum changes from one expression to another, based on Tai's approach.

Example Expressions

We will use these example expressions in the following considerations:

expr1 = a[b[c[d]], e[f[g, h]], i, j]; expr2 = r[s[t[u, v], w, x], y[z]]; expr3 = a[b[c, d], e]; expr4 = x[y[z]]

Ordering

First one needs a way to obtain the parts of an expression in a particular order. The order chosen is given by the preorder traversal of trees, since this will prove to be a rather natural input for functions defined later.

preorder[expr1, "Labels" -> True]

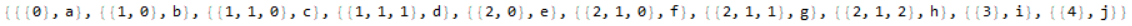
The "Labels" option is False by default, naturally yielding an output that contains only the positions of the parts of the expression.

Ancestry

The notion of node ancestry will be important to define for expressions. Luckily we need only consider ancestry in terms of descendants, which is far easier to implement.

Descendants

Keeping the visual conventions of tree representation in mind, the descendants of a node are simply the other nodes in the tree that can be connected by a path that only travels down from the source node. One need not define a function to find descendants, all one needs is a function that can confirm if one position could possibly be the descendant of another. For example, the node at some position {1, 0} might have descendants whose positions begin with a 1, but the node at position {2, 1} cannot possibly be a descendant.

Edit Operations

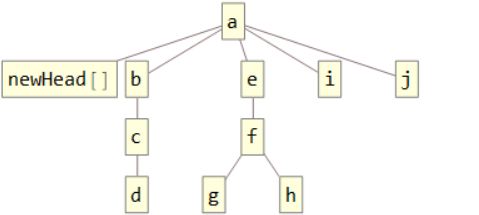
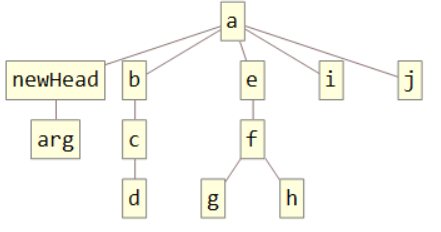
For the most part, the built-in edit operations Delete, Insert and ReplacePart suit the needs of this problem. However Insert has been altered slightly to insertElement so that expressions that will be heads in the future are inserted with appended empty brackets. The following is a demonstration of this functionality.

ClearAll[temp]; temp = expr1; TreeForm[temp = insertElement[temp, newHead, {1, 0}], AspectRatio->0.5]

TreeForm[insertElement[temp, arg, {1, 1}], AspectRatio -> 0.5]

Generating Mappings

Mapping Validity

In defining a function to obtain valid mappings from one expression to another, one must keep in mind the criteria for mapping validity:

• Mappings must be one-to-one
• Mappings must preserve the ordering of nodes
• Mappings must preserve the ancestry of nodes

The form chosen to represent mappings is an association, with keys being source positions, pointing to values which are target positions.

validMappings = mappings[expr3, expr4]

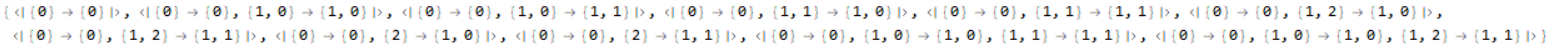The way to read a mapping is simple: the keys are positions in the source expression and the values positions in the target expression. The presence of a key/value pair indicates a replacement operation, the absence of a source position from the keys indicates a deletion and the absence of a target position indicates an insertion.

Mapping Length

Let the mapping length equal the number of operations implied by a mapping. For example, the mapping that only indicates replacing the root of expr3 with that of expr4 has a length of 7, since after the replacement, we delete the remaining arguments of the expression's head, then insert the node y followed by the node z.

Optimal Mappings

The symbolic edit distance is simply the least number of edits one must perform on one expression to turn it into another. From the definition of mapping length, it follows that the symbolic edit distance is simply the mapping length of the most optimal mapping. For expr3 and expr4 the symbolic edit distance is 4, and that is achieved by all of the valid mappings above, apart from the first one.

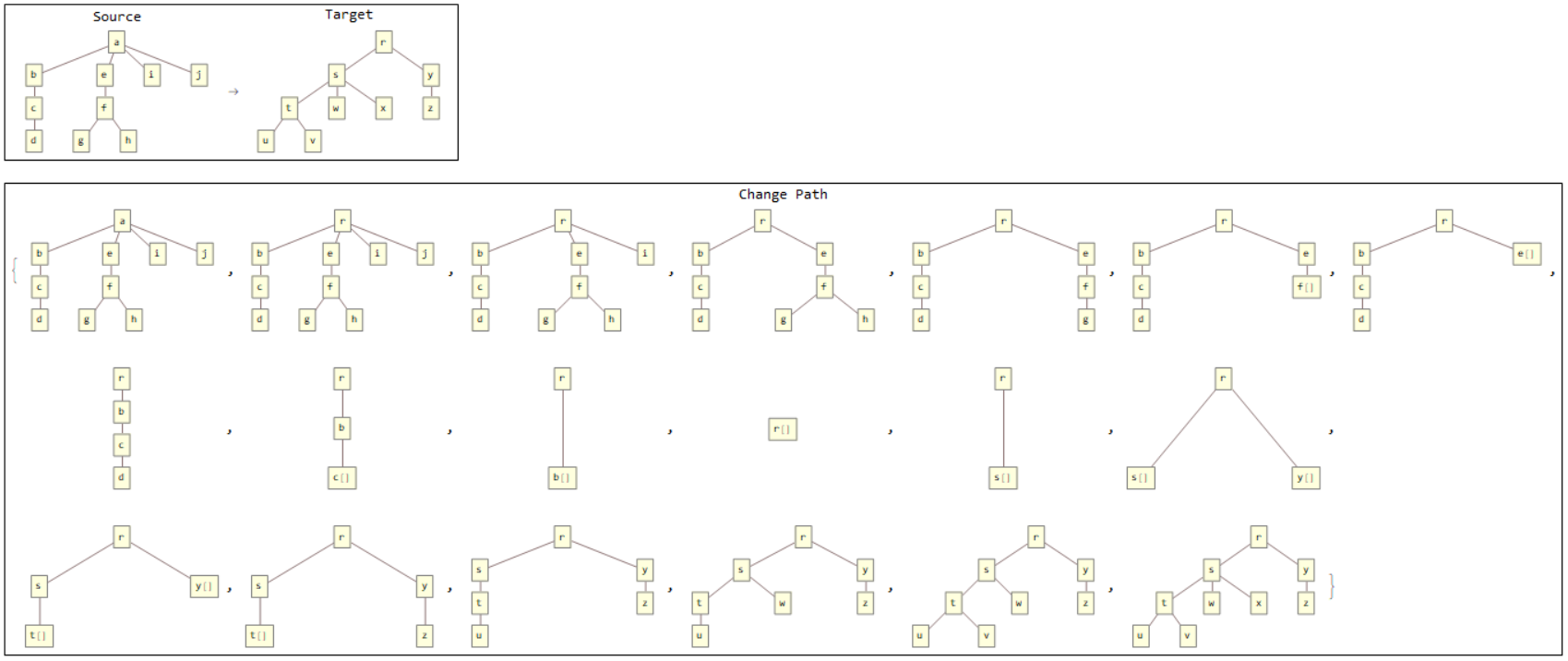
Change Paths

From Mappings to Change Paths

Generating a change path is as simple as first replacing the labels of source nodes, whose positions are the keys of the mapping, with their respective target nodes, whose positions are the values of the keys, then deleting the source nodes whose positions are not keys in the mapping and finally by inserting target nodes whose positions are not values in the mapping.

mapping = RandomChoice[validMappings]
path = changePath[expr3, expr4, mapping]
TreeForm[#, AspectRatio->0.5]&/@path

Minimum Change Paths

Generating the minimum change path is as simple as using only the most optimal mapping in the function changePath. This is precisely the functionality of minChangePath.

minPath = minChangePath[expr3, expr4]
TreeForm[#, AspectRatio->0.5]&/@minPath

Problems

• While we can find the optimal mappings given by normal graph theory, there is currently no insert function that can perform what I call "intermediate node insertion", that is, inserting a node between a parent and one or more of its children, so that a subset of the children of the parent node become the children of the inserted node. This means that some mappings cannot currently be used to generate change paths. A possible resolution to this problem would be to create a function capable intermediate node insertion, but such a function would actually represent a compound edit operation, not a single operation. Alternatively we could keep this almost built-in version of node insertion and simple change the criteria for mapping validity.
• The current way in which mappings are searched for is highly memory intensive. So much so that for expressions only slightly larger than those used as examples, the client simply wont execute a search for valid mappings. One possible solution to this would be to simple eliminate mappings which one knows will yield inefficient change paths.

References

1. K.-C. Tai. The tree-to-tree correction problem.
2. K.Zhang and D.Shasha. Simple fast algorithms for the editing distance between trees and related problems.
3. E.D. Demaine, S. Mozes, B. Rossman and O. Weimann. An optimal decomposition algorithm for tree edit distance.