Introduction
Suppose one wants to know the average temperature throughout a time series. With the existing resources, the only option is to calculate the average of every single data point for the entire time interval. This option, however, is extremely inefficient as every point is needed in order to generate the average. To solve this problem, we examine how we may divide the time series into years, months, weeks, dates, and hours so that when the average is calculated, we can simply extract the temperature values for the years, months, etc. and reduce the number of objects that is needed for the average to be calculated. I will start by extracting the complete years that occur during this time series. By doing so, we created objects that will represent all the data points for that year. We may then continue this process and extract the complete months from the time that does not assemble a complete year. Then, we continue this process by grouping the dates that are left into combinations of six - day weeks and days.
Time Series Summarization
I have decided that I will write out the time series as a combination of years, months, weeks, days, and hours. The logic that I will use to break down a time series will be the following:
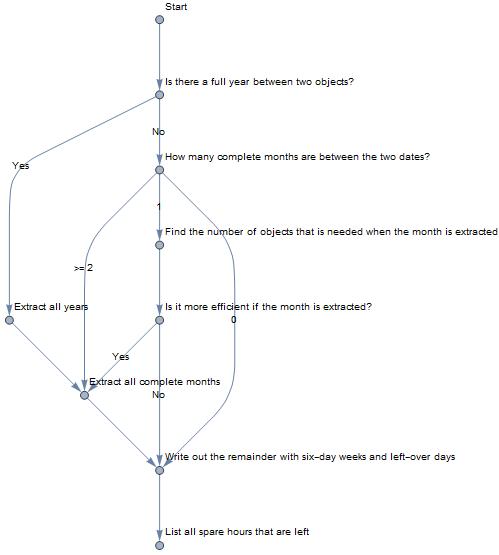
Notice that one unique feature of my optimization model considers six-day weeks instead of the traditional seven-day format. I have decided to do so for several reasons:
- It is actually more efficient to write out time series combinations when the weeks are six days long. I wrote the program that will determine for week length of n days how many week/day objects will be needed to assemble a time series of m days for all m that is less than the max number of days in a month (Thus, 1 <= m <= 30). When I sum of all the number of objects needed across all m values for each of the n values, I realized that n=6 actually has the lowest total, which means that n = 6 will be the most efficient. Also, it takes less objects to assemble periods of 30, 31 days when n=6 because 6 divides these values almost evenly.
- This will eliminate any potential for the need to reconsider the optimization strategy for the beginning and the ending of the time series: If the traditional seven-day week format is used, then the optimizing strategy will take one extra step because if we consider the time series [June 1st, July 5th], then grouping this time series into 5 weeks instead of the month of June plus 5 days will mean that less objects is needed when we calculate the average. Using the six-day week format will eliminate such concerns. Once we extracted the weeks and dates, we will create the most efficient combination for this time series.
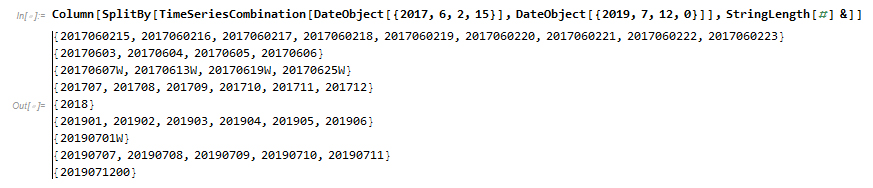
Based on the tree diagram, I can go ahead and assemble the most efficient combination. I will construct the TimeSeriesCombination to obtain the most optimal time series combination.The following is a combination of years (expressed as yyyy, where yyyy stands for the year), months (yyyymm), weeks (yyyymmddW), dates (yyyymmdd), hours (yyyymmddhh), expressed in chronological order.
TimeSeriesCombination[DateObject[{2019, 6, 2, 1}],
DateObject[{2019, 7, 5, 0}]]
{"2019060201", "2019060202", "2019060203", "2019060204",
"2019060205", "2019060206", "2019060207", "2019060208", "2019060209",
"2019060210", "2019060211", "2019060212", "2019060213", "2019060214",
"2019060215", "2019060216", "2019060217", "2019060218", "2019060219",
"2019060220", "2019060221", "2019060222", "2019060223", "20190603W",
"20190609W", "20190615W", "20190621W", "20190627W", "20190703",
"20190704", "2019070500"}
To make this time series more readable, we can go ahead and group it by the type of object. In this case, all consecutive hours will be grouped together, than days, weeks, etc.
Evaluation: In Application To Weather Data
Using this optimized time series summarization, I can find the maximum, minimum, and the mean air temperature for a time series. For now, the functions only apply to Waltham, MA. An extra parameter will be needed to allow users to select their locations. The temperature interval can be determined by looking at the objects generate by the TimeSeriesCombination function and using these as keys to search up generated weather temperature data (I have created a data file producing process that is intended to improve the Wolfram Knowledge Base) and using the weather temperature data to calculate the overall maximum, minimum, and mean value during this time interval.
MaxTemperatureInterval[DateObject[{2016, 8, 13, 0}],
DateObject[{2018, 2, 23, 23}]]
Quantity[81.788, "DegreesFahrenheit"]
MinTemperatureInterval[DateObject[{2016, 8, 13, 0}],
DateObject[{2018, 2, 23, 23}]]
Quantity[0.710001, "DegreesFahrenheit"]
MeanTemperatureInterval[DateObject[{2016, 8, 13, 0}],
DateObject[{2018, 2, 23, 23}]]
Quantity[48.5953, "DegreesFahrenheit"]
Evaluation: How Efficient Is This Function?
We decided to conduct a test to see how much the generated function improves the overall efficiency of finding data of that time series. We determine how time, in seconds, it takes for the algorithm we determined, and also the existing algorithm, to determine the mean temperature throughout 300 time series, each ending at 2018/12/31 but have lengths of 1 day, 2 days, ... We find that initially the existing method is more efficient. However, as the number of days increase my method starts to prevail. 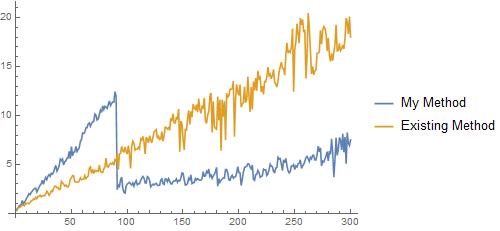
Based on the plot, we can see that past 90 days my function will be significantly more efficient than the existing method. I anticipate that as the number of days increase, my method will become more and more efficient compared to the existing method.
Why This Function Is Actually More Important Than Just The Efficiency
To double check that my code makes sense, I go back to check the calculated value against the value that is calculated using the existing method. When I look at the values, there seems to be some differences.  The difference is even bigger when we are looking at smaller time intervals.
The difference is even bigger when we are looking at smaller time intervals.  While I wonder what is causing this difference, I remembered my initial experiment on time series and remembered that the number of data points for each day is not equal:
While I wonder what is causing this difference, I remembered my initial experiment on time series and remembered that the number of data points for each day is not equal:
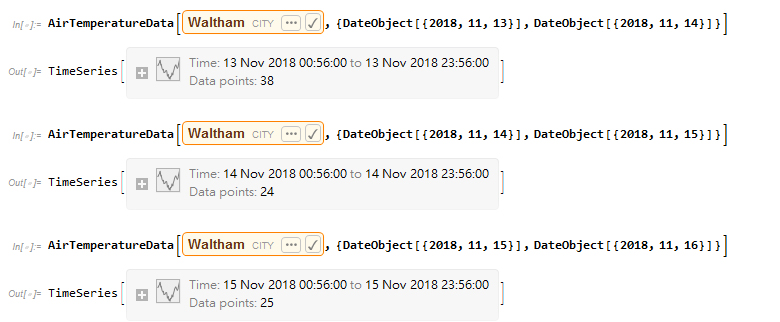 Using the data files that I have, I calculated and confirmed that the existing system simply takes all the data points during that time interval and averages it out. What this means is that the mechanism will favor some mechanisms over the others. In the case between 2018/11/13 to 2018/11/15, the temperature is larger because the date, whose temperature is 46.5 F (higher than the other two dates) is favored during the calculation. Thus, my method of calculation will provide a more calculation of the mean because every day will have the same weight during the calculation. Note that my mechanism is not perfect. This comes from the fact that the daily temperatures are calculated with the same method that caused the inaccuracies in the existing mechanism, and the unequal representation of hours is a glaring issue in calculating daily temperatures:
Using the data files that I have, I calculated and confirmed that the existing system simply takes all the data points during that time interval and averages it out. What this means is that the mechanism will favor some mechanisms over the others. In the case between 2018/11/13 to 2018/11/15, the temperature is larger because the date, whose temperature is 46.5 F (higher than the other two dates) is favored during the calculation. Thus, my method of calculation will provide a more calculation of the mean because every day will have the same weight during the calculation. Note that my mechanism is not perfect. This comes from the fact that the daily temperatures are calculated with the same method that caused the inaccuracies in the existing mechanism, and the unequal representation of hours is a glaring issue in calculating daily temperatures:
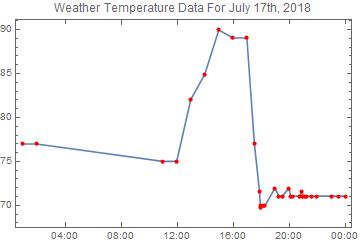
In this case, the temperature during 2:00 and 10:00 is not even calculated! When calculating averages, 18:00-24:00 will be heavily favored and the mean temperature for the date will be a lot close to the 70 F mark as a result. Thus, daily temperatures should eventually be calculated by averaging the values for all the hours.
Future Work
I can examine whether inserting other time intervals (quarters, decades, centuries, minutes, seconds) will allow for an even more efficient processing, and implement these intervals if it is indeed more efficient to do so. I can also use the time series summation to look at other data (Dow Jones index, etc.) to generate relevant statistical analysis such as forecasting.
Further Exploration
GitHub link: https://github.com/altan4377/WSS-2019