Introduction

The goal of this project is to find ways to go from specific cellular automata (CA) rules to other rules with similar behavior. Currently, the only way to effectively find behavior of CA's is to run them over some amount of steps until clear patterns of behavior emerge. This means that the only practical way to find CA's with particular properties is to search for them over the space of all possible CA rules. However, it is often the case that some CA's with rules close to each other will have similar behavior. It is unclear what the relation between changing rules and changing behavior is, if there even is any. So, the aim of this project is to find methods to make small changes in the behavior of cellular automata based on their rules.

Methodology

To find CA's that are close to each other in the space of rules of the same form - meaning the same possible colors and radius of cells that determine the following cells - the basic idea is to find the least significant pieces of a rule and change them incrementally. The rule of a CA is defined by a series of blocks representing all possible color sequences of the rule's radius, each associated with one color for the block to be replaced by in the next iteration of the automata. So, the least significant piece of the rule is taken to be the rule that is applied least over some run of the automata. This can easily be measured by searching each row of the CA for occurrences of each rule block and totalling them over the CA. Then, blocks of arbitrary significance can be iteratively changed by changing the color of one block at a time, then changing the next least significant block in the same way. This continues recursively for some specified number of block replacements.

Implementation

(* constants *)
size=50; (* size of square CA's to be tested *)
colors=3; (* possible colors for CA *)
radius=1; (* radius of rule - 1 is nearest neighbor, 2 is next-nearest, etc. This is really slow if it's bigger than 1 *)
max=colors^colors^(2radius+1); (* max rule number in base 10 *)
initial=RandomInteger[colors-1,size]; (* random initial condition *)
ruleLen=colors^(2radius+1); (* number of blocks (possible replacements) in rule *)

(* CA base functions *)
getRule[]:=RandomInteger[{0,max-1}] (* randomly select a rule *)
getBlocks[]:=Tuples[Reverse[Range[0,colors-1,1]],2radius+1] (* all blocks of cells in the rule *)
ruleDigits[rule_]:=ruleDigits[rule]=IntegerDigits[rule,colors,ruleLen] (* rule in base of # colors *)
cellGrid[rule_]:=cellGrid[rule]=CellularAutomaton[{rule,colors,radius},initial, size-1] (* matrix containing colors of CA after set number of steps *)
showRule[rule_]:=RulePlot[CellularAutomaton[{rule,colors,radius}]] (* get ruleplot *)
showCA[rule_]:=ArrayPlot[cellGrid[rule]] (* show CA with rule number, visual rule, and visual grid *)
compressionRatio[ca_]:=N[ByteCount[ca]/ByteCount[Compress[ca]], 4] (* ratio of uncompressed to compressed size of CA, good measure for classification *)
difference[rule_,newRule_]:=Total[Abs[countUses[rule]-countUses[newRule]]] (* measure of difference between rules by summing squares of differences between rule applications - currently unused *)

(* rule incrementing functions *)
ruleShift[rule_,block_,shift_]:=ruleShift[rule,block,shift]=FromDigits[Mod[IntegerDigits[rule,colors,ruleLen]+SparseArray[block->shift,ruleLen],colors],colors] (* change the color of one replacement from the rule *)
countUses[rule_]:=countUses[rule]=Lookup[Counts[Flatten[Partition[cellGrid[rule],{1,3}],2]],getBlocks[],0] (* count uses of each block of the rule in a ca *)
blockOrder[rule_,blocks_,distance_]:=Ordering[countUses[rule],blocks+distance][[distance+1;;]] (* order of blocks to be replaced *)
shifts[rule_,block_]:=ruleShift[rule,block,#]&/@Table[i,{i,colors-1}] (* shift one block of  *)
iterateRules[rule_,reps_]:=Map[rule->iterateRules[#,Rest[reps]]&,shifts[rule,First[reps]]] (* make a tree of associations for all specified rule replacements *)
iterateRules[rule_,{}]:=rule (* recursive base case *)
connections[rule_]:=iterateRules[rule,blockOrder[rule,blocks,distance]]//.Rule[a_,{b__Rule}]:>{Rule[a,#]&/@Keys[{b}],b}//Flatten//DeleteDuplicates (* make map suitable for graphing *)

Visualization

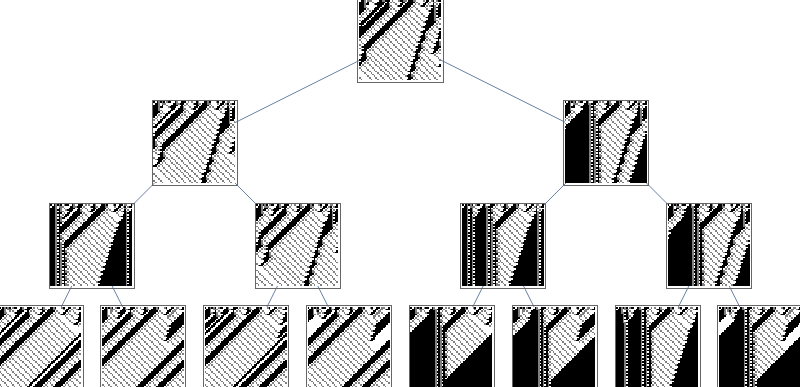Figure 1. Changing three blocks of a CA

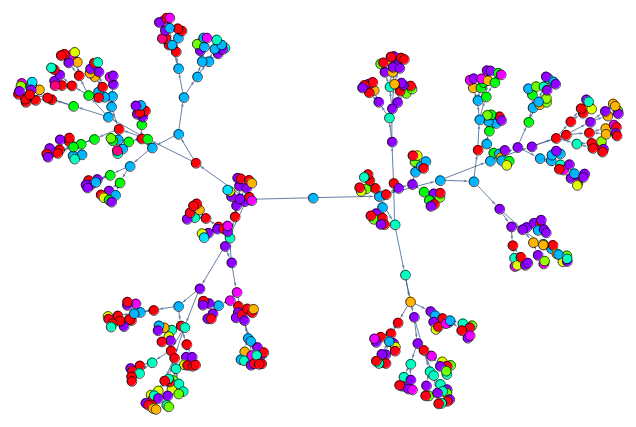
Figure 2. Network showing changes of eight blocks for a CA - colors are a measure of each rule's behavior based on amount of repetition

Conclusions

This project focused on three-color CA's whose rules depended only on each cell's nearest neighbors, as the space of two-color nearest-neighbor CA's is too small to see incremental behavior changes. This method does work for an arbitrary number of colors and radii, however increasing either of these means that many more replacements must be done to see noticeable changes in behavior. The run time of the rule incrementing algorithm increases very rapidly as more blocks are replaced, so only a small portion of the rule space can be covered from any class of automata other than two-color nearest-neighbor.

The current method of finding CA's with specified behavior is only to search through as many possible rules as possible and try to find, visually or computationally, which ones have behavior close to what is desired. Using this algorithm, the process could be highly streamlined by starting from a rule with some known behavior and trawling through similar rules. The amount of similarity between each rule iteration can also be specified, so rules with significantly different behaviors can also be found easily.

Future Work

This algorithm also allows for the possibility of machine learning using CA's, as rules can be iteratively changed to descend along a gradient of rule behaviors. The CA parallel of a derivative can be defined for this purpose as the relation between the distance between rules, given by the number of replacements and how significant they are, and the change in behavior, which can be found somewhat accurately from the amount of compression possible for some run of each CA.

This method of iterating rules can also be applied to other types of replacement systems using the same idea of changing parts of the substitution rule that are applied least (or most), only requiring the algorithm to search and replace differently depending on the system. However, it could probably be generalized to all rule-based systems.