With the equational theorem proving framework in Wolfram Language, it is easy to check the correctness of a theorem with a machine-generated proof. However, such proofs almost always involve extremely lengthy and convoluted lemmas that are incomprehensible for human readers. In my project, I implemented a set of functions that can provide a step-by-step reduction of Boolean algebra expressions. The functions recursively apply heuristic rules to expressions until they reach normal form. Moreover, the functions can return the shortest reduction between any two equivalent Boolean algebra expressions by a dynamic version of Dijkstra's algorithm.

What can my functions do

Given an arbitrary Boolean expression, I can give a step-by-step reduction of it to normal form.

reduceList[DNF][and[or[a, b], b]] // generateProofNotebook

I can give a shortest step-by-step reduction.

reduceShortestList[DNF][and[or[a, b], b]] // generateProofNotebook

I can convert an expression in conjunctive normal form ("and" of "or") to disjunctive normal form ("or" of "and"), or the other way around:

generateProofNotebook /@ {reduceShortestList[CNF][or[and[a, not[b]], and[not[b], c]]],
reduceShortestList[DNF][and[not[b], or[a, c]]]}

Or a shortest path between any two equivalent Boolean expressions:

How do the functions do that

To provide a short step-by-step reduction of Boolean expressions, there are two major steps:

• identify potential application of heuristic rules and apply them
• find the shortest sequence of rule applications to reduce a Boolean expression to normal form

The identification functions use pattern matching, the applications functions use substitution frameworks, and the search for shortest path uses a dynamic version of Dijkstra's algorithm.

Setting up: symbols I use for Boolean algebra

Since Mathematica evaluates inputs upon entering them, we use the lower case version of Boolean literals and operators, namely "true", "false", "and", "or", and "not". We regard commutativity as a trivial property of "and" and "or" and set their attributes to be Orderless.

SetAttributes[and, Orderless];
SetAttributes[or, Orderless];

Identify Patterns and Apply Rules

List of heuristic rules I use

The set of heuristic logic equivalence rules I used are:

png

Identify one potential step of a given pattern and apply it

dentify all potential steps of a given pattern on the outermost level

Identify all potential steps of a given pattern on all levels

Reduce an expression to normal form

Find Shortest Reduction

Graph of Boolean Expressions

I can regard every Boolean expression as a vertex, and I claim that two Boolean expression vertices are adjacent if one can be transformed into another by one heuristic step. Then I have a graph of Boolean expressions, where each connected components is an equivalence class of Boolean expressions.

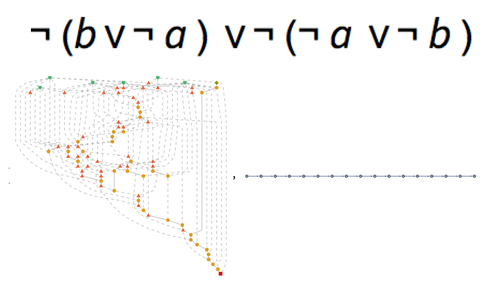
Each edge can be denoted in the form of {curr, prev, step}, where "curr" and "prev" are two Boolean expressions such that "curr" can be derived by applying step to "prev". Here is a graph of all first-order neighbors to the expression

Challenges to Dijkstra's Algorithm

Dijkstra's Algorithm

Dijkstra's Algorithm is a classic algorithm for finding the shortest path between any two vertices in a connected graph.

1. Potentially Infinite Size of Graph

The size of any connected component in a Boolean expression graph is infinite. For any expression e, you can easily find countably infinite equivalent expressions just be adding arbitrarily many double negations ahead of it. (You can easily find uncountably many by alternating between double negation and identity rules.) It is impossible to know how large the graph needs to be so that a path exists between two equivalent expressions. Since the framework for graphs in Wolfram Language can only handle static finite graphs, I cannot use the built-in "FindShortestPath" function.

2. Computationally Irreversible Equivalence Rules

Every step we take in reducing Boolean expressions is invertible, but only in theory. If we have the expression p[And][Not]p , we can easily reduce it to

Solutions to the Challenges

Examples

Generating Notebooks of Proofs

What I want my functions to do in the future

1. Potential improvements in the algorithm:

2. Explorations in multilevel logic reduction:

Appendix

Conversion between formats

SetAttributes[and, Orderless];
SetAttributes[or, Orderless];

<<Notation`
InfixNotation[ParsedBoxWrapper["\[And]"],and]
InfixNotation[ParsedBoxWrapper["\[Or]"],or]
Notation[ParsedBoxWrapper[RowBox[{"\[Not]", "x_", " "}]] \[DoubleLongLeftRightArrow] ParsedBoxWrapper[RowBox[{" ", RowBox[{"not", "[", "x_", "]"}]}]]]

and[or[not[and[not[a],b]],c],b]

PNG

Identify Steps

Helpers

indices[e_]:= Range[Length[e]]
pairs[set_]:= Subsets[set,{2}]
select[list_,test_,All]:= Select[list,test]
select[list_,test_,n_]:=S elect[list,test,n]
unequal[e_]:= e=!=#&

Recursive Handle

(*
recursion returns step structures of a given pattern from all levels of a given expression
input:
	opt_: All or 1;
	find_: a find function for a particular pattern, e.g. findDoubleNegation;
	e_: a boolean expression;
output:
 	if opt is 1, returns one potential step of the given pattern from some layer of the expression
	if opt is all, returns all potential step of the given patternfrom all layers of the expression
	returns {} if no potential steps of the given pattern exist in any layer of the expression
*)
recursion[opt_][find_][e_]:= Join[find[opt][e],Sequence @@Table[Append[Most[#],Prepend[Last[#],i]]&/@recursion[opt][find][e[[i]]],{i,1,Length[e],1}]]

Pattern Finding Functions

(*
find functions returns step structures of the given pattern from the outermost layer of a given expression
input:
	opt_: All or 1;
	e_: a boolean expression;
output:
 	if opt is 1, returns one potential step of the given pattern from the outermost layer of the expression
	if opt is all, returns all potential step of the given pattern from the outermost layer of the expression
	returns {} if no potential steps of the given pattern exist in the outermost layer of the expression
*)
identifyLiteral[and,true]:= "Identity";
identifyLiteral[and,false]:= "Domination";
identifyLiteral[or,true]:= "Domination";
identifyLiteral[or,false]:= "Identity";
identifyLiteral[not,true]:= "False";
identifyLiteral[not,false]:= "True";
identifyLiteral[_,_]:= {}
findLiteral[opt_][e_]:=select[indices[e],e[[#]]==true||e[[#]]==false&,opt]//Map[{identifyLiteral[e[[0]],e[[#]]],ToString[e[[0]]],{#}}&]

findIdempotent[opt_][e_]:=select[pairs[indices[e]],e[[#[[1]]]]===e[[#[[2]]]]&,opt]//Map[{"Idempotent",{#}}&]

findNegation[opt_][e_]:=select[pairs[indices[e]],(e[[#[[1]]]]==not[e[[#[[2]]]]]||not[e[[#[[1]]]]]==e[[#[[2]]]])&,opt]//Map[{"Negation",ToString[e[[0]]],{#}}&]

findDoubleNegation[opt_][not[not[_]]]:={{"Double Negation",{}}}
findDoubleNegation[_][_]:={}

findDeMorgan[_][not[and[__]]] := {{"De Morgan","and",{}}}
findDeMorgan[_][not[or[__]]] := {{"De Morgan","or",{}}}
findDeMorgan[_][_] := {}

findOrDistributive[opt_][or[terms__]]:=select[indices[{terms}],({terms}[[#]][[0]]===and)&,opt]//Map[Table[{"Distribution",or,i,#,{}},{i,select[indices[{terms}],unequal[#],opt]}]&]//Flatten[#,1]&
findAndDistributive[opt_][and[terms__]] :=select[indices[{terms}],({terms}[[#]][[0]]===or)&,opt]//Map[Table[{"Distribution",and,i,#,{}},{i,select[indices[{terms}],unequal[#],opt]}]&]//Flatten[#,1]&
findOrDistributive[_][_] := {}
findAndDistributive[_][_] := {}

findAssociative[opt_][or[terms__]]:=select[indices[{terms}],({terms}[[#]][[0]]===or)&,opt]//Map[{"Association",{#}}&]
findAssociative[opt_][and[terms__]]:=select[indices[{terms}],({terms}[[#]][[0]]===and)&,opt]//Map[{"Association",{#}}&]
findAssociative[_][_] :={}

matching[list1_,list2_]:=Flatten[Table[{#,i}&/@list1,{i,list2}],1]
findElementInTerm[terms_,ele_]:=SelectFirst[List@@terms,ele== #&,{}]
findAbsorption[opt_][and[terms__]]:=With[{orTerms=Select[indices[{terms}],{terms}[[#,0]]== or&]},
select[matching[orTerms,indices[{terms}]],findElementInTerm[{terms}[[#[[1]]]],{terms}[[#[[2]]]]]=!={}&,opt]]//Map[{"Absorption",Sequence@@#,{}}&]
findAbsorption[opt_][or[terms__]]:=With[{andTerms=Select[indices[{terms}],{terms}[[#,0]]== and&]},
select[matching[andTerms,indices[{terms}]],findElementInTerm[{terms}[[#[[1]]]],{terms}[[#[[2]]]]]=!={}&,opt]]//Map[{"Absorption",Sequence@@#,{}}&]
findAbsorption[_][_]:={}

Potential Step

(*
findPotentialStep returns potential steps of any pattern from any layer of a given expression
input:
	opt_: All or 1;
	seq_: CNF, DNF, or full;
	e_: a boolean expression;
output:
 	if opt is 1, returns one potential step of any pattern from some layer of the expression
	if opt is all, returns all potential step of all patterns from all layers of the expression
	returns {} if no potential steps of any given pattern exist in any layer of the expression, this happens when the expression is in normal form 
*)
CNF = {findDoubleNegation,findLiteral,findDeMorgan, findAssociative,findIdempotent, findOrDistributive,findNegation,findAbsorption};
DNF = {findDoubleNegation,findLiteral,findDeMorgan, findAssociative,findIdempotent, findAndDistributive,findNegation,findAbsorption};
full = Union[CNF,DNF];
findPotentialStep[seq_][1][e_] := Module[{result},SelectFirst[seq,(result = recursion[1][#][e])=!={}&,{}];first[result]]
findPotentialStep[seq_][All][e_] :=Join@@Table[recursion[All][find][e],{find,seq}]

Apply Steps

Helpers

(* these helper functions add options to replace or extract entire expressions *)
replacePart[e_,{}->new_]:= new
replacePart[e_,loc_->new_]:= ReplacePart[e,loc->new]
extract[e_,{}]:= e
extract[e_,loc_]:= Extract[e,loc]
reduceSingle[e_]:= If[Length[e]<=1,e[[1]],e]

Apply Step

(* applyStep takes a boolean expression and a step, and returns a boolean expression with the step applied*)
applyStep[e_,{}]:={}
applyStep[e_,{"Identity",_,loc_}]:=replacePart[e,Most[loc]->(Drop[extract[e,Most[loc]],{Last[loc]}] // reduceSingle)]
applyStep[e_,{"Domination","and",loc_}]:=replacePart[e,Most[loc]-> false]
applyStep[e_,{"Domination","or",loc_}]:=replacePart[e,Most[loc]-> true]
applyStep[e_,{"True",_,loc_}]:=replacePart[e,Most[loc]->true]
applyStep[e_,{"False",_,loc_}]:=replacePart[e,Most[loc]->false]
applyStep[e_,{"Idempotent",loc_}]:= replacePart[e,Most[loc]->(Drop[extract[e,Most[loc]],{Last[loc][[1]]}] // reduceSingle)]
applyStep[e_,{"Negation","and",loc_}]:= replacePart[e,Most[loc]-> false]
applyStep[e_,{"Negation","or",loc_}]:= replacePart[e,Most[loc]-> true]
applyStep[e_,{"Double Negation",loc_}] := replacePart[e,loc->extract[e,Join[loc,{1,1}]]]
applyStep[e_,{"De Morgan","and",loc_}]:=replacePart[e,loc->or @@not /@ extract[e,loc][[1]]]
applyStep[e_,{"De Morgan","or",loc_}]:=replacePart[e,loc->and @@not /@ extract[e,loc][[1]]]
applyStep[e_,{"Distribution",oper_,left_,right_,loc_}]:=Module[{smaller,bigger,orig,dropped,new},
{smaller,bigger}=Sort@{left,right};
orig=extract[e,loc];
dropped=Drop[#,{smaller}]&@Drop[#,{bigger}]&@ orig;
new= oper[orig[[left]],#]&/@orig[[right]];
replacePart[e,loc->(Append[dropped,new]//reduceSingle)]]
applyStep[e_,{"Association",loc_}]:=replacePart[e,Most[loc]->Join[Drop[extract[e,Most[loc]],{Last[loc]}],extract[e,loc]]]
applyStep[e_,{"Absorption",tIndex_,eIndex_,loc_}]:=replacePart[e,loc->(Drop[extract[e,loc],{tIndex}]// reduceSingle)]

Reduce Expressions

Helpers

first[{}] = {}; 
first[list_] := First[list]; 
last[{}] = {}; 
last[list_] := Last[list]; 

Reduce Expressions with a List of Steps

(*
reduceList returns a list of steps and expressions that reduces the given boolean to CNF or DNF;
input:
	seq_: CNF or DNF;
	e_: a boolean expression;
output:
 	a list of {expression, location, rule} 
*)
reduceList[seq_][e_]:=
NestWhileList[With[{trans=findPotentialStep[seq][1][#[[1]]]},{applyStep[#[[1]],trans],#[[1]],trans}]&,{e,{},{"Initial",{}}},#[[1]]=!={}&]
reduceListExpression[seq_][e_]:=NestWhileList[applyStep[#,findPotentialStep[seq][1][#]]&,e,#=!={}&]
reduceExpression[seq_][e_]:=reduceListExpression[seq][e][[-2]]

Find Shortest Path

Find Shortest Path

shortestRoute[e1_,e2_]:=Reverse[Switch[reduceExpression[CNF][e1]==reduceExpression[CNF][e2],True,findShortestRoute[e1,e2],False,{}]]

findShortestRoute[e1_,e2_]:=Module[{edges1={{e1,{},{"Initial",{}}}},edges2={{e2,{},{"End",{}}}},meet},
NestWhile[({edges1,edges2}={expandEdges[edges1],expandEdges[edges2]})&,{},(meet=findCommonEdge[edges1,edges2])==={}&];
Join[tracePath[edges1,meet[[1]],{meet[[1]]}],reverseTracePath[tracePath[edges2,meet[[2]],{meet[[2]]}]]]]//DeleteCases[#,x_List/;Length[x]==0]&

reduceShortestList[seq_][e_]:=findShortestRoute[e,reduceExpression[seq][e]]

Helper for Visualization

displayList[list_]:=list//Map[{first[last[#]],last[last[#]],first[#]}&]//TableForm
graph[edges_]:=Graph[#[[2]]->#[[1]]&/@DeleteCases[edges,a_List/;a[[3,1]]=="Initial"]]

Operations on Edges

Find Membership in Edges

(*
FindMemberInEdges checks if an expression is already in the list of edges. 
input:
	edges_: a list of edge structures;
	new_: an Boolean expression;
output:
 	{} if new is not already in edges;
 	the corresponding edge structure of new if new is already in edges.
*)
findMemberInEdges[edges_,new_]:=SelectFirst[edges,First[#]== new&,{}]

Find Intersection in Edges

(*
FindCommonInEdges checks if two list of edges has intersection. 
input:
	n1, n2: two lists of edge structure;
output:
	{} if intersection is empty;
	a edge structure in the intersection if intersection is not empty.
*)
findCommonEdge[n1_,n2_]:=Module[{m1,m2},m1=SelectFirst[n1,(m2=findMemberInEdges[n2,First[#]])=!={}&,{}];Switch[m1,{},{},_,{m1,m2}]]

Union Edges

(*
JoinEdges joins a edge structure into a list of edge structure if it is not already in. 
input:
	edges: a list of edge structures;
	new: a edge structure;
output:
	the original edges list if new is already in edges;
	the original edges list with new appended if new is not already in edges.
*)
joinEdges[edges_,new_]:=Switch[findMemberInEdges[edges,First[new]],{},Append[edges,new],_,edges]
(*
UnionEdges merge two list of edges and removes duplicates from the new list. 
input:
	old: a list of edge structures;
	new: a list of edge structures in which duplicates will be removed;
output:
	a merged list of edge structures
*)
unionEdges[old_,new_]:=Fold[joinEdges,old,new]

Expand Edges

findAllEdges[e_] := {applyStep[e,#],e,#}&/@findPotentialStep[full][All][e]
expandEdges[edges_]:=unionEdges[edges,Flatten[findAllEdges[#[[1]]]&/@edges,1]]

Trace Path

tracePath[_,{},trace_]:= trace
tracePath[edges_,end_,trace_]:=With[{lastEdge=findMemberInEdges[edges,end[[2]]]},tracePath[edges,lastEdge,Prepend[trace,lastEdge]]]

Reverse Path

reverseTracePath[edges_]:=Reverse[reverseEdge/@ edges]
reverseEdge[{curr_,prev_,{"Initial",{}}}]:={curr,prev,{"Initial",{}}}
reverseEdge[{curr_,prev_,{"End",{}}}]:={curr,prev,{"End",{}}}
reverseEdge[{curr_,prev_,{"Identity",oper_,loc_}}]:={prev,curr,{"Identity'",oper,Most[loc]}}
reverseEdge[{curr_,prev_,{"Domination",oper_,loc_}}]:={prev,curr,{"Domination'",oper,Most[loc]}}
reverseEdge[{curr_,prev_,{"False",oper_,loc_}}]:={prev,curr,{"False'",oper,Most[loc]}}
reverseEdge[{curr_,prev_,{"True",oper_,loc_}}]:={prev,curr,{"True'",oper,Most[loc]}}
reverseEdge[{curr_,prev_,{"Idempotent",loc_}}]:={prev,curr,{"Idempotent'",Most[loc]}}
reverseEdge[{curr_,prev_,{"Negation",oper_,loc_}}]:={prev,curr,{"Negation'",oper,Most[loc]}}
reverseEdge[{curr_,prev_,{"Double Negation",loc_}}]:={prev,curr,{"Double Negation'",loc}}
reverseEdge[{curr_,prev_,{"De Morgan",_,loc_}}]:={prev,curr,{"De Morgan'",loc}}(* change for better explanation *)
reverseEdge[{curr_,prev_,{"Distribution",oper_,tIndex_,eIndex_,loc_}}]:={prev,curr,{"Distribution'",loc}}(* change for better explanation *)
reverseEdge[{curr_,prev_,{"Association",loc_}}]:={prev,curr,{"Association'",Most[loc]}}
reverseEdge[{curr_,prev_,{"Absorption",_,_,loc_}}]:={prev,curr,{"Absorption'",loc}}
reverseEdge[_]:={}