Nehal,
One (not very computationally efficient) way to do this
paths = {{a, e, f}, {a, b, c}, {a, i, l, j, f}, {a, e, h, g, d}, {a,
i, m, q, o, j, f}, {a, i, l, n, k, h, f}, {a, i, l, n, k, g,
d}, {a, i, l, j, h, g, d}, {a, e, j, n, k, g, d}, {a, i, m, r, u,
t, o, j, f}, {a, i, m, r, u, p, n, j, f}, {a, i, m, r, u, p, k, h,
f}, {a, i, m, r, u, p, k, g, d}, {a, i, m, q, t, p, n, j, f}, {a,
i, m, q, t, p, k, h, f}, {a, i, m, q, t, p, k, g, d}, {a, i, m, q,
o, n, k, h, f}, {a, i, m, q, o, n, k, g, d}, {a, i, m, q, o, j, h,
g, d}, {a, i, l, o, t, p, k, h, f}, {a, i, l, o, t, p, k, g,
d}, {a, e, j, o, t, p, k, g, d}, {a, i, m, s, v, u, t, o, j,
f}, {a, i, m, s, v, u, p, n, j, f}, {a, i, m, s, v, u, p, k, h,
f}, {a, i, m, s, v, u, p, k, g, d}, {a, i, m, r, u, t, o, n, k, h,
f}, {a, i, m, r, u, t, o, n, k, g, d}, {a, i, m, r, u, t, o, j, h,
g, d}, {a, i, m, r, u, p, n, j, h, g, d}, {a, i, m, q, t, p, n, j,
h, g, d}, {a, i, l, o, q, r, u, p, k, h, f}, {a, i, l, o, q, r, u,
p, k, g, d}, {a, e, j, o, q, r, u, p, k, g, d}, {a, e, j, l, m, r,
u, p, k, g, d}, {a, e, j, l, m, q, t, p, k, g, d}, {a, i, m, s, v,
u, t, o, n, k, h, f}, {a, i, m, s, v, u, t, o, n, k, g, d}, {a, i,
m, s, v, u, t, o, j, h, g, d}, {a, i, m, s, v, u, p, n, j, h, g,
d}, {a, i, l, o, q, s, v, u, p, k, h, f}, {a, i, l, o, q, s, v, u,
p, k, g, d}, {a, e, j, o, q, s, v, u, p, k, g, d}, {a, e, j, l, m,
s, v, u, p, k, g, d}}
nodeLabels = paths // Flatten // Union;
nodeCount = nodeLabels // Length;
indexes = Map[ToString /* LetterNumber, paths, {-1}];
matrix = Map[SparseArray[# -> ConstantArray[1, Length@#]] & /* Normal /* (PadRight[#, nodeCount] &), indexes];
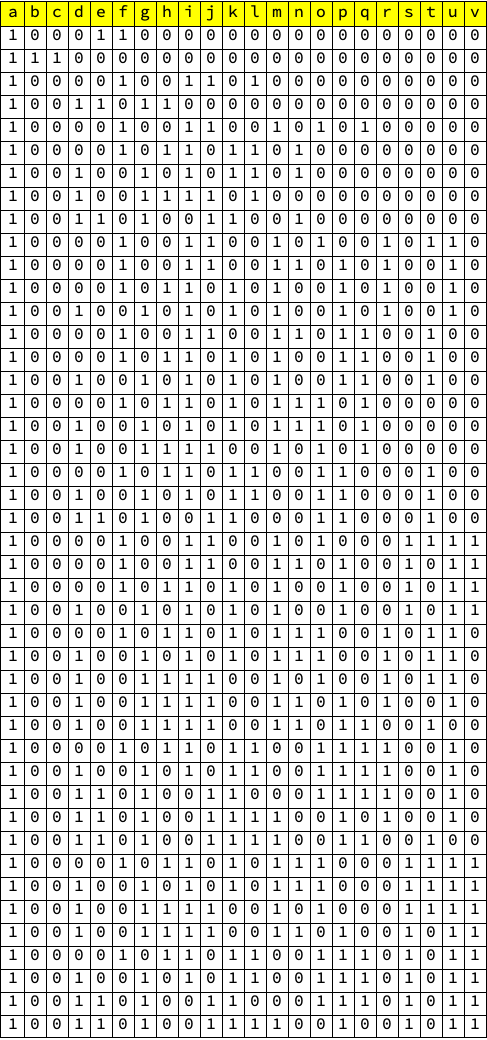
Grid[matrix // Prepend[nodeLabels], Frame -> All, Background -> {Automatic, {1 -> Yellow}}]