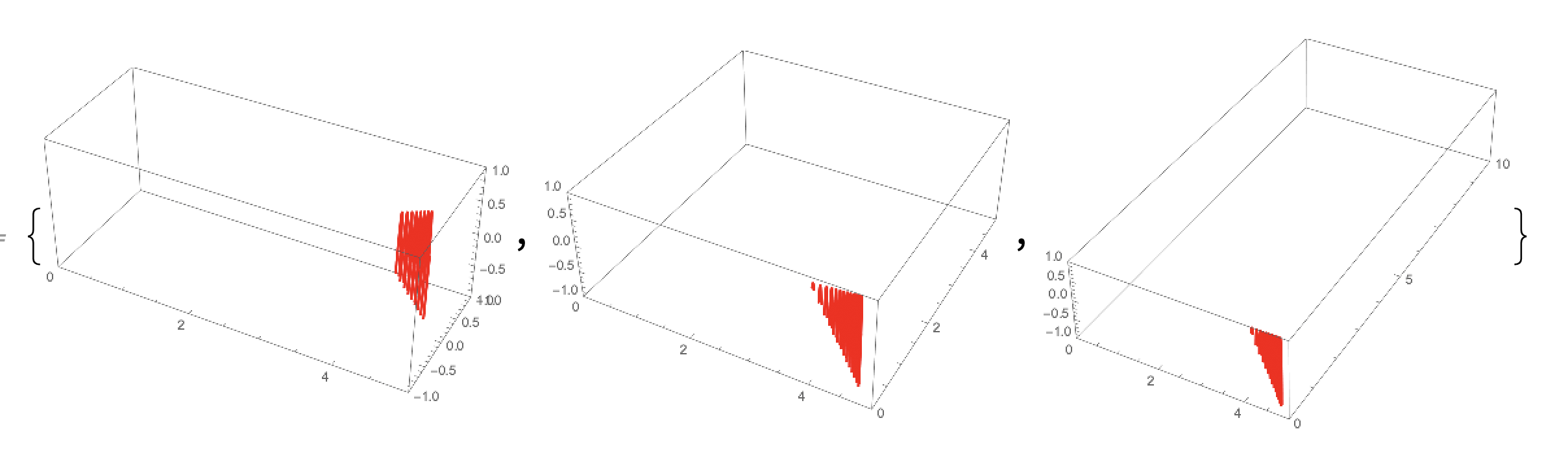
Overview

Differential equations are very useful in modelling complex systems that change with time. For this exploration, the differential equation we are looking at has a particular form: x''[t]+x'[t]==f[x[t]], where f is a real-valued function. The goal of this project is to investigate different behavior of these equations and to be able to classify them using supervised machine learning to classify different behaviors.

Chaotic Behaviours of Differential Equations

One way to visualize this chaotic behavior is to use phase portrait. Phase portraits show how a function, its derivative, and its second derivative are changing. Here is an example: the solution to x’’[t]+x’[t]==Sin[Exp[x[t]] seems to exhibit chaotic behavior in range {t,0,15}: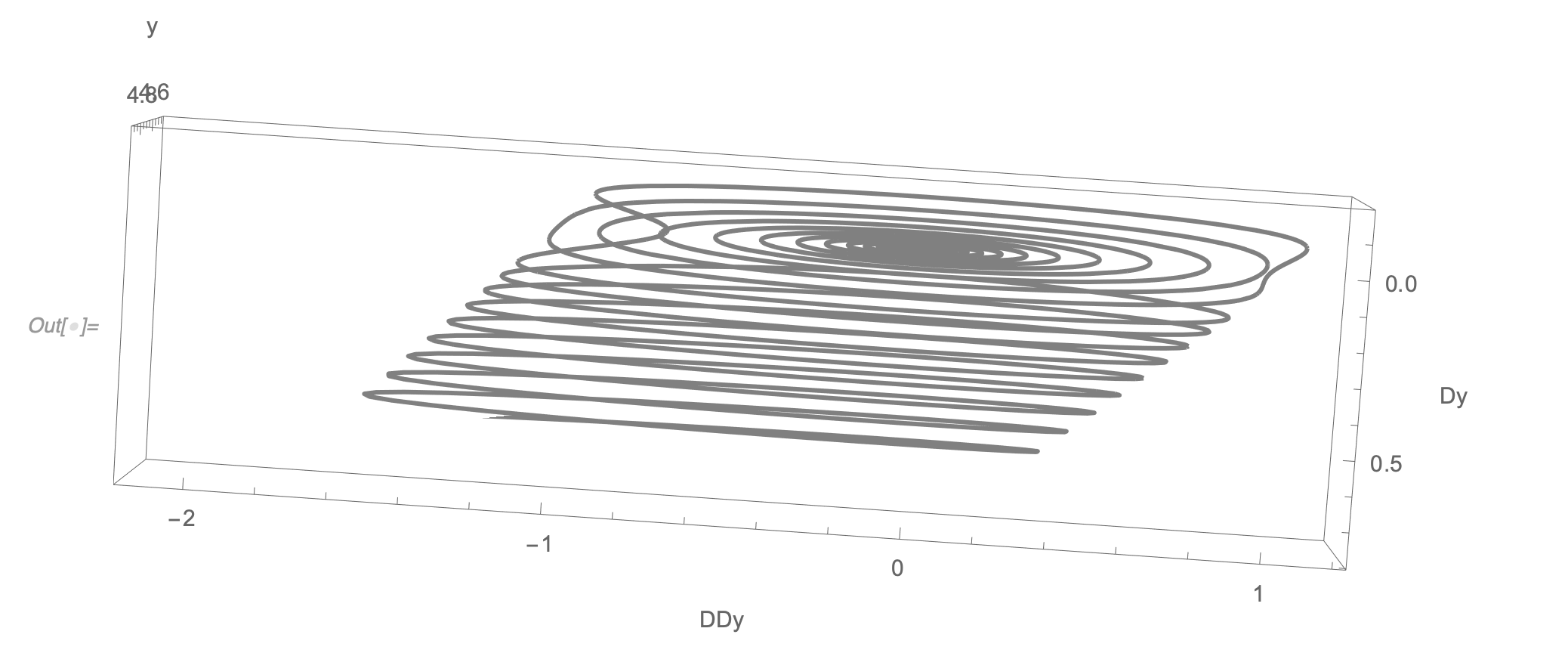

Euclidean Distance Test

We can calculate the distances between two points in phase portrait. With a successive collection of sample points, the result is a series of distances. If a graph converges, the sequence will converge to zero. The successive differences of the sequence will also go to zero. Note it is necessary to divide the terms by their distance to the origin in case the point is far away from origin. Here is one example of the output, which is the plot of a list of differences of distance sequence/distance from origin, as compared to its behavior.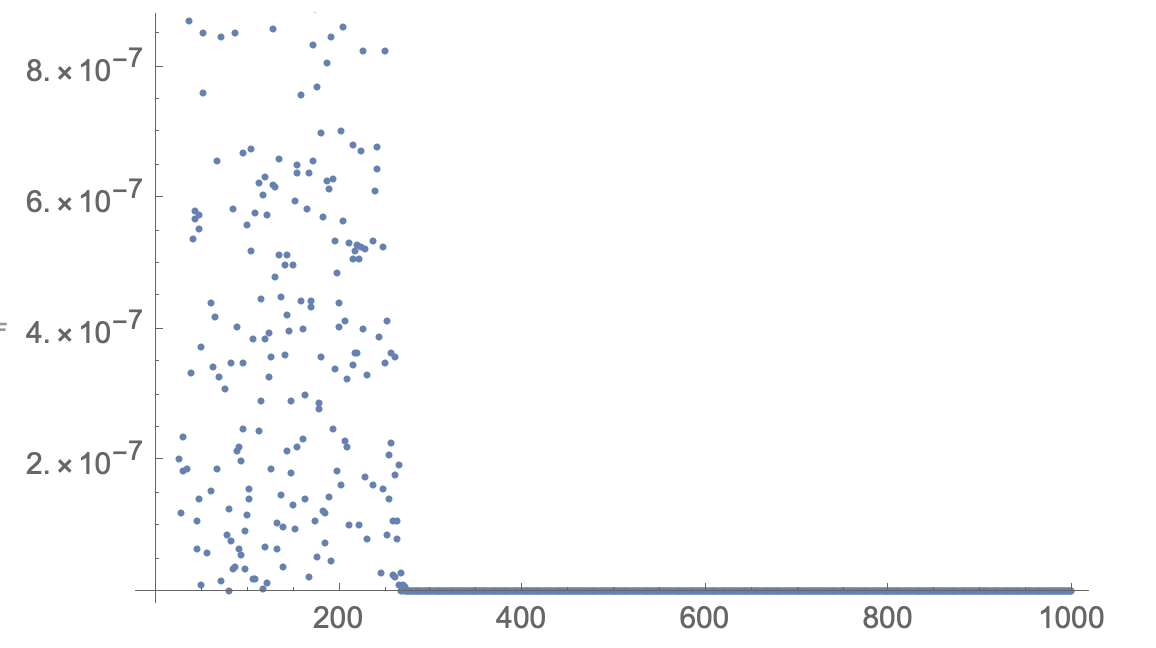

Classify and Machine Learning

The following graphs are the result extracted from one thousand differential equations with the form x''[t]+x'[t]==f[x[t]]. These graphs are divided into 9 classes representing different behaviors.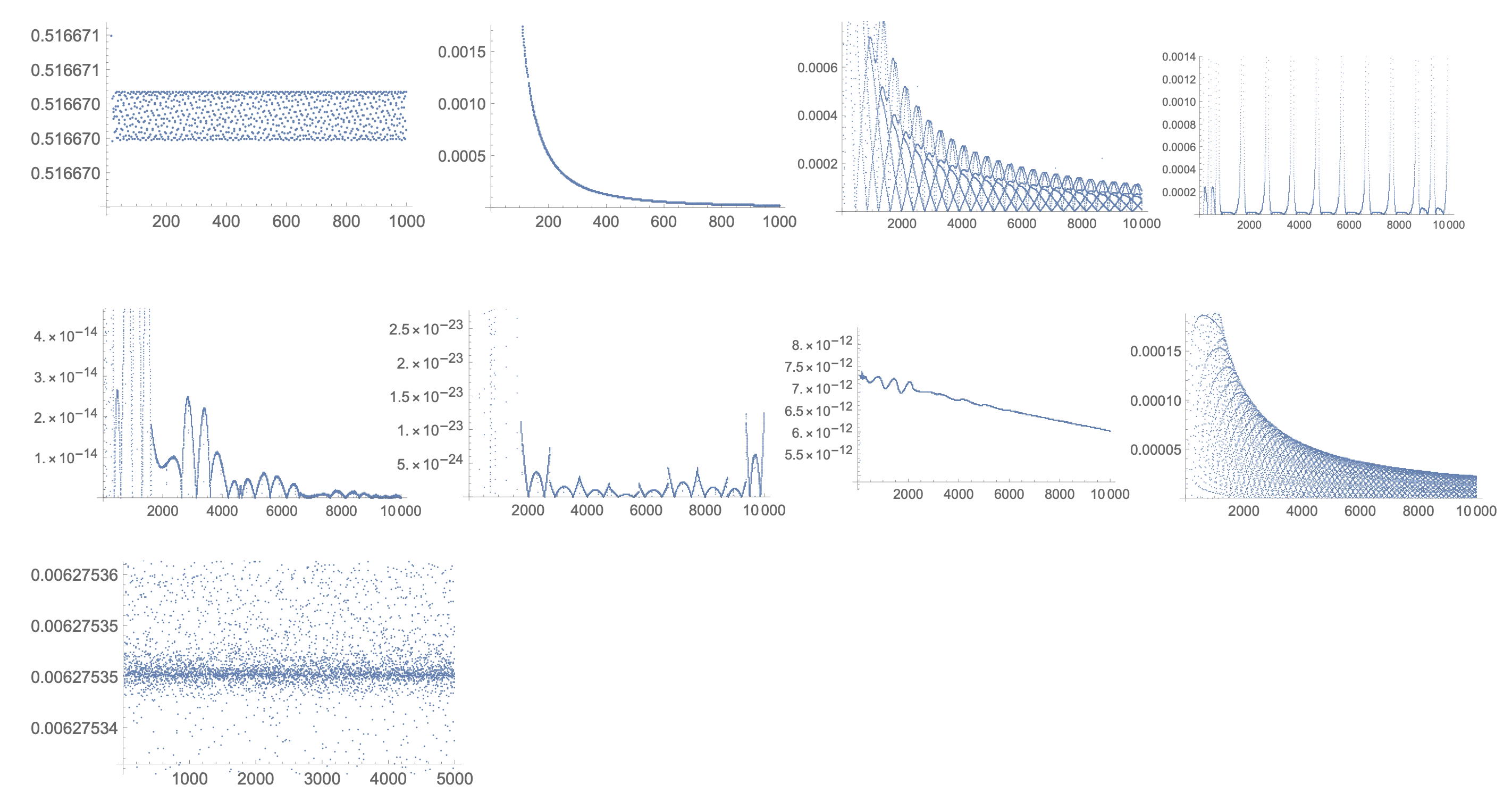

Under the assumption that changing the initial condition of the differential equation just slightly will result plots in same classes, 700 random training data are generated to train the machine. Each data is scaled by a random amount to avoid bias.The result shows that this algorithm has an accuracy of 99.0%+/- 1.6%.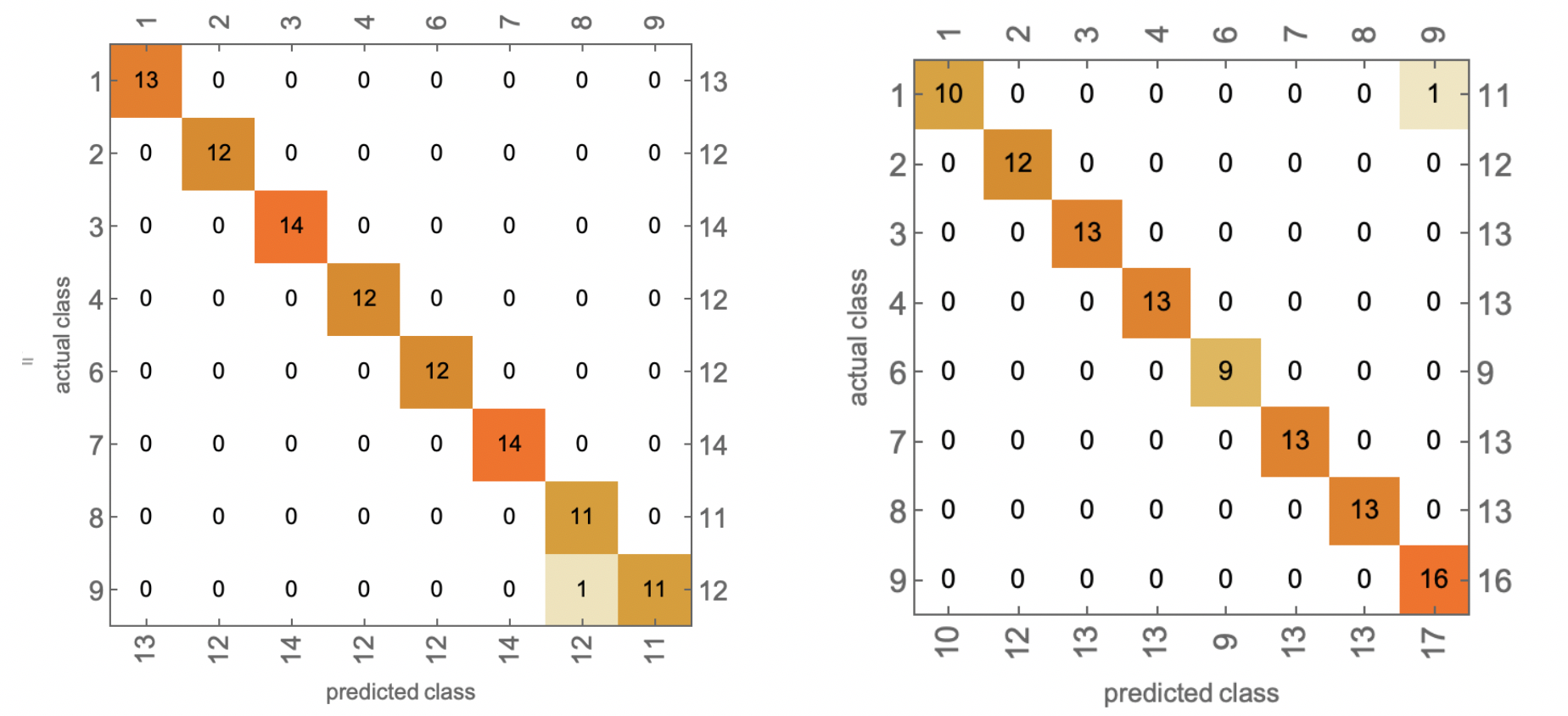

Conclusion

Throughout this project, I successfully detected the chaotic behavior of different differential equations and classified them. The output includes a function that generate the phase portrait of some differential equations, a function that tells the interval in which the function is chaotic for input function continuous on the input interval. Finally, there is a machine learning classification that can classify different behaviors of chaotic functions with accuracy about 99%.

Github Link