Introduction

Text analysis provides insight into stories that can be difficult to parse, especially when they are sufficiently large. This project aims to make a program that can use text analysis on any play in order to evaluate the relationships between characters. One can use sentiment analysis on each sentence and incorporate the frequency of these sentiments to determine a relationship's health. Then, a graph with vertices representing the characters and edges representing their relationships illustrates the entire social network. The health of these relationships can be visualized with color, and frequency with width. Further operations with graphing functions can provide information on local groups within the play. In addition, accounting for who speaks to who, visualized with directed edges, allows for nuanced relationships in which feelings are not mutual.

In order to test the universality of my program, I analyzed 10 plays of various time periods: Hamlet, King Lear, Midsummer Night’s Dream, Romeo and Juliet, The Tempest, Oedipus the King, Oedipus at Colonus, Antigone, Death of a Salesman, and The Glass Menagerie. Each play is given custom values for a negativity bias, positive tolerance, and negative tolerance so that the final graph best illustrates the play:

(* Set conditions specific to play: {play number, negativity bias, 
positive tolerance, negative tolerance} *)
playConditions = 
  Table[plays[[i]] -> {i, 1, .30, -.30}, {i, 1, 
    Length[plays]}]; (* Default Setting *)
exceptions = {Values[playConditions[[1]]] -> {1, 1.2, .20, -.30}, 
   Values[playConditions[[2]]] -> {2, 1.35, .30, -.20},
   Values[playConditions[[3]]] -> {3, 1.25, .40, -.30}, 
   Values[playConditions[[4]]] -> {4, 1.3, .30, -.30}, 
   Values[playConditions[[5]]] -> {5, 1.3, .30, -.30}, 
   Values[playConditions[[6]]] -> {6, 1.3, .30, -.30},
   Values[playConditions[[7]]] -> {7, 1.3, .30, -.30}, 
   Values[playConditions[[8]]] -> {8, 1.3, .35, -.30}, 
   Values[playConditions[[9]]] -> {9, 1.3, .30, -.20}, 
   Values[playConditions[[10]]] -> {10, 1.3, .30, -.30}};
playConditions = playConditions /. exceptions;

This project can be divided into two subtasks. The first is to accurately identify the speaker and recipient of a sentiment. The next is to incorporate numerous sentiment values to assess the overall health of a relationship between each pair of two characters.

Determining the Characters Involved

First, correctly identifying the speaker can be easily done for plays, as each speaker is bolded:

speakerOrder = 
  Capitalize[
   ToLowerCase@
     StringCases[text, Shortest["<b>" ~~ x__ ~~ "</b>"] -> x] // 
    Flatten, "AllWords"];
nameList = speakerOrder // DeleteDuplicates;

This code captures the speaker of each line, which allows us to split up the text into lines of the speakers. The sentences of each line correspond to the speaker of the line, and they are then split in preparation of individual sentiment analysis:

lines = StringSplit[
     text // StringDelete[Shortest["<i>" ~~ x__ ~~ "</i>"]] // 
      StringDelete[Shortest["[" ~~ x__ ~~ "]"]], 
     Shortest["<b>" ~~ x__ ~~ "</b>"]] // 
    StringDelete[Shortest["<" ~~ x___ ~~ ">"]] // Rest;
sentences = lines // TextSentences;
lineLength = Length /@ sentences;

Determining the recipient of a sentiment requires making a few assumptions. The recipient of each sentence is initially set to the speaker of the previous line. Then, searching in the order of sentences, a character name within a sentence reassigns the sentiment to the corresponding character for that sentence and all the following sentences in the same line. Finally, the list of speakers for each sentence is directed to the list of recipients of each sentence. Searching for names can be accomplished as the following:

emphasis = 
  WordFrequency[Flatten[sentences], #, IgnoreCase -> True] & /@ 
   nameList;
diffRecipientPos = SortBy[Position[emphasis, _?Positive], Last];

Calculating the Health of Relationships

First, we complete sentiment analysis on each sentence:

feelings = 
  Classify["Sentiment", #, "Probabilities"] & /@ sentences // Flatten;

Using individual sentiments to judge overall relationship health, I assumed that a large number of nonstandard probabilities indicate health, and the more numerous these probabilities are the more reflective they become of the relationship. Experimentally, I created a formula which punishes uncertainty, and rewards frequency:

{pos, neu, neg} = 
  Table[feelings[[i]][#], {i, 1, Length[feelings]}] & /@ {"Positive", 
    "Neutral", "Negative"};
negBias = Values[playConditions][[playNum]][[2]];
Health = (pos - negBias*neg)/(1 + neu);
sentenceHealth = {finalRules[[#]], Health[[#]]} & /@ 
   Range[Length[Health]];
sentenceHealthFormat = Cases[sentenceHealth, {#, _}] & /@ ruleList;
relationshipHealth = 
  Table[Mean[
    Table[sentenceHealthFormat[[i]][[j]][[2]], {j, 1, 
      Length[sentenceHealthFormat[[i]]]}]], {i, 1, 
    Length[sentenceHealthFormat]}];
(* Incorporate Frequency into Health *)
freq = Table[
   Length[sentenceHealthFormat[[i]]], {i, 1, 
    Length[sentenceHealthFormat]}];
freqMultiplier[x_] := (Log[x] + 2)/2;

Generating the Relationship Graph

The positive and negative tolerance values filter out neutral and conflicted sentiments. The calculated health of each relationship can be converted into a color ranging from red to green. Blending with gray allows one to more easily visualize health as brightness instead of color:

viableRel = 
  Position[relationshipHealthFinal, 
    x_ /; x > posTolerance || x < negTolerance] // Flatten;
relationshipHealthFinalExc = 
  Table[relationshipHealthFinal[[i]], {i, viableRel}];
viableFreq = Table[freq[[i]], {i, viableRel}];
relationshipColors = 
 Table[Blend[{Red, Gray, Green}, (i + 1)/2], {i, 
   relationshipHealthFinalExc}]
viableEdges = Table[ruleList[[i]], {i, viableRel}];
edgeColors = 
  Table[viableEdges[[i]] -> relationshipColors[[i]], {i, 
    Length[viableEdges]}];

Producing a community graph plot illustrates clusters of characters with strong feelings toward each other (not necessarily positive):

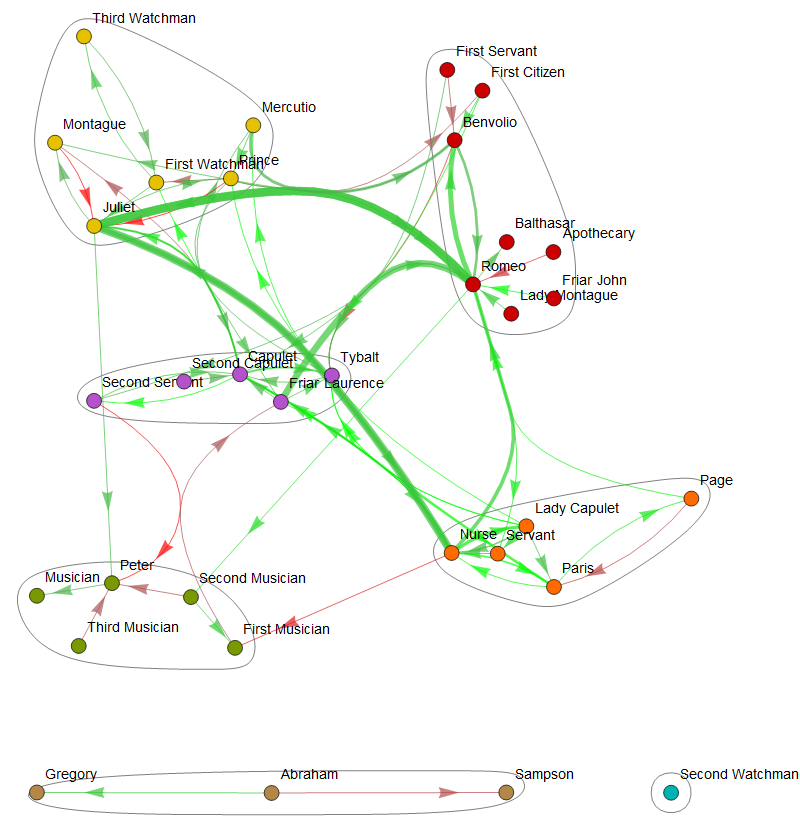
Conclusion

The necessity of a negativity bias suggests that the Wolfram sentiment classifier may have a positivity bias. Also, by human evaluation of the plays and the respective relationship network graphs, Shakespearean works appear to generate the most accurate graphs. This may be due to the text structure of the different time periods: perhaps using sentiment analysis on each sentence was too large of a unit for Greek plays that employ long, winding sentences, and too small for modern plays that utilize rapid, stichomythic dialogue and interjections.

Extension

As such, the size of the text used for each calculation of sentiment could be a function of sentence length. Additionally, setting the values for health parameters can be automated. Furthermore, one could handle the cases of having multiple recipients for a sentiment. The most difficult avenue, though perhaps the most fruitful, would be to catch pronouns, aliases, and titles and assign them to the proper recipient. Once completed, a novel can be analyzed by using a similar process to determine the speaker in addition to the recipient of a particular sentiment.