Introduction
Will programs ever be able to write other programs? This question is a discussion point where the halting problem is a significant argument against it. But could we already use machine learning techniques to simplify the daily routine of programmers? We think, yes.
Problem
The problem of applying the machine learning algorithms such as neural networks to the source code is that the source code is not a numerical thing. We need to map the programming code to real numbers. Such a transformation is called an embedding.
Code Embeddings
How should this transformation look like? For example, we can split the code into pieces and apply one-hot encoding where each element of a vector is associated with exactly one element. But would it be effective? The source code of programs is not random data, it is a sequence of commands with some structure, and an embedding must utilise the structure of the code as much as possible. 
What is this project about
In our project, we tried to explore different forms of embeddings for Wolfram Language. And then, use this representation to find similar built-in functions. For this purpose, we gathered a lot of samples of code in Wolfram Language from different sources. Then we cleaned the samples and made them interpretable. We trained a couple of classical neural network architectures with various parameters to find vector representation for built-in functions in Wolfram Language. Also, we did experiments with a state-of-the-art method in source code embeddings. The details are explained in the following.
In this post, we present only snippets of our solution, all sources are available on GitHub: https://github.com/ckorikov/WSS-19.
Dataset
The success of machine learning tasks depends heavily on the quality of the data. There was no ready dataset for this task. We started collecting it by ourselves. To build a dataset we used three sources:
- all the Wolfram Mathematica documentation,
- the Mathematica's internal unencrypted files
- and 923 GitHub repositories as large as ~57Gb.
File-based cache. Extracting data from sources is a long-running process. That is why we needed to have a mechanism which could recover data if the procedure is interrupted. The following code shows our implementation of the file-based cache. We used the Wolfram exchange format as a file format to serialize every piece of data.
SetAttributes[keyValueStore, HoldRest];
keyValueStore[expr_, default_:None] := With[
{path = FileNameJoin[{$cachePath, IntegerString[Hash[expr], 36] <> ".wxf"}]},
Replace[
Quiet @ Import[path, "WXF"],
_?FailureQ :> With[
{evaluated = default},
Export[path, evaluated, "WXF"];
evaluated
]
]
]
Source 1. Wolfram Mathematica documentation. Wolfram Mathematica provides a convenient way to access documentation data with help of WolframLanguageData function. It is known that the documentation contains a lot of samples of usage of built-in functions. We would like to get these examples. To do this we apply the following function to every keyword of Wolfram Language.
getSourceFromDocExample[EntityValue[WolframLanguageData[symbol],"DocumentationExampleInputs"]]
where symbol is the name of requested documentation of the keyword. In getSourceFromDocExample we extract data from input cells and transform them into expressions as follows
Cell[BoxData[r_], "Input", ___] :> MakeExpression[r, StandardForm]
Source 2. Internal unencrypted files. Here, we searched Wolfram Mathematica system files in the $InstallationDirectory directory.
wlFiles=FileNames["*.wl",$InstallationDirectory,Infinity];
mFiles=FileNames["*.m",$InstallationDirectory,Infinity];
Then we excluded apriori inappropriate files like files from AutoCompletionData directory or SearchIndex manually. After this, we extracted expressions from every file. The main logic is in the following code where the path is a full file path.
List @@ Map[
HoldComplete,
Replace[
Quiet@ToExpression[
StringReplace[
ReadString[path],
{
Shortest["Package["~~___~~"]"]-> ""
}
],
InputForm,
HoldComplete
],
{
h_HoldComplete :> DeleteCases[h, Null],
_ :> HoldComplete[]
}
]
]
You can notice a replacement in the code.
"Package["~~___~~"]"]-> ""
It is needed to overcome the incorrect behaviour of ToExpression function which load Package instead of converting it to expression.
Source 3. GitHub repositories. Data from GitHub repositories were downloaded with the help of the GitHub API. We tried to get all repositories which were written in Wolfram Language. GitHub sets mark "Mathematica" for such repositories. Also, we restricted ourselves with a timeout to avoid download repositories with colossal size. Finally, we got 923 GitHub repositories as large as ~57Gb. After cleaning auxiliary files and we got only 317 Mb of *.m files. We used the script for Wolfram Mathematica system files to extract expressions from the repositories.
After merging samples from 3 sources we have a dataset containing 464 991 valid Wolfram Mathematica expressions in HoldComplete form. In the dataset, column "source" shows either file path for system files and GitHub repositories, either function name for data from the official documentation. The "index" represents a position of the expression inside the corresponding source.

To sum up, as the first step in the project, we gathered a dataset of code in Wolfram Language from three different sources. We came across several problems. Firstly, it is a continuation of the data gathering after fail which is solved with the file-based cache. Secondly, the code in Wolfram Language cannot be just loaded into Wolfram Mathematica because the system always tries to evaluate expressions, so we had to wrap every piece of our processing logic with HoldComplete. Thirdly, there was found a bug in ToExpression related to the processing of Wolfram Language packages, which we solved with ad-hoc exclusions manually. An example of the dataset is shown above.
Models
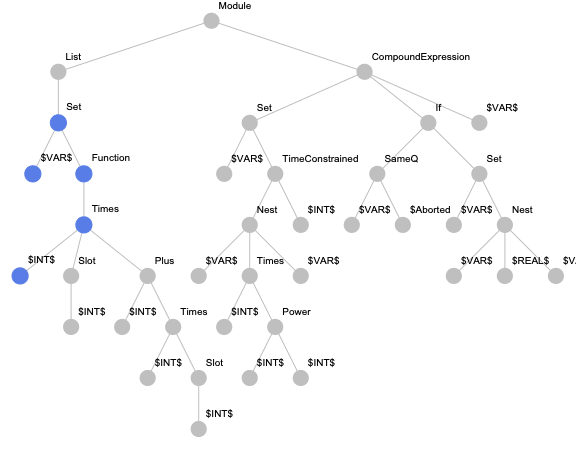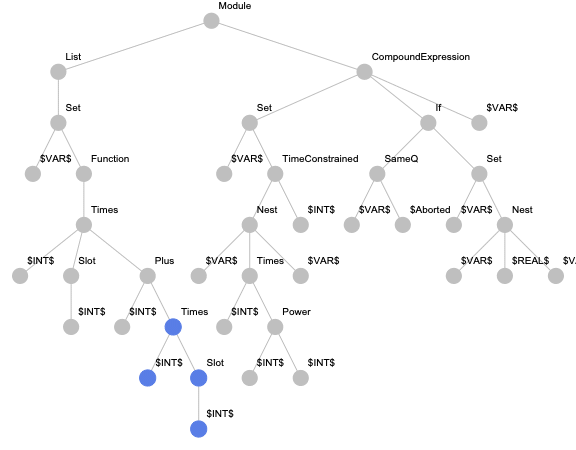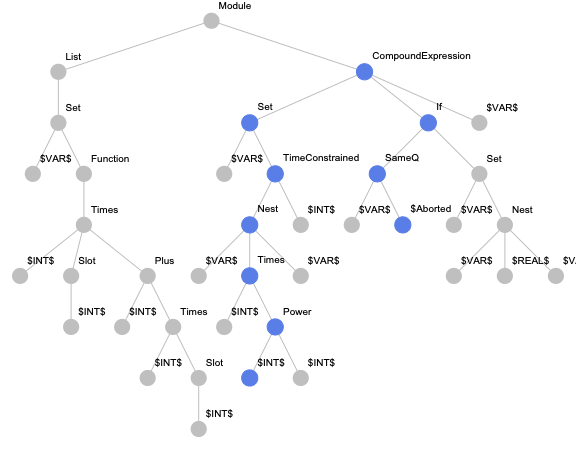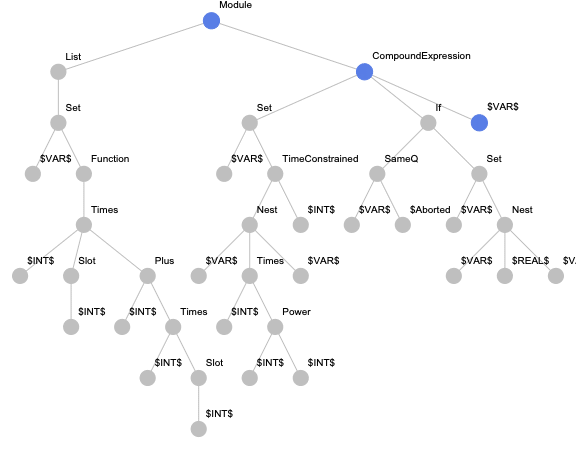
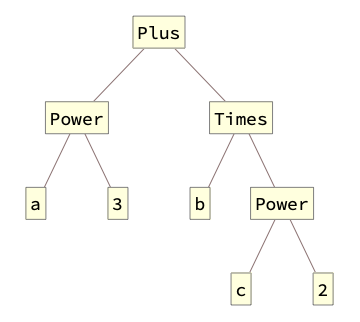
According to modern research, source code can be mapped in vector space with different granularity. For instance, It can be applied a linguistic approach to code when it is considered as a text. In this case, the character level granularity is used. But for source code, it is more meaningful to use token level granularity. Also, a source code representation should capture the structure of the program as much as possible. It is usually implied a tree structure of code. Next picture shows the tree structure of Wolfram Language expression.
a^3 + b c^2
There are different approaches that allow building a model of code. For simplicity, we started from a well-known method statistical language modelling.
Statistical language modelling
This method allows us to develop a probabilistic model that is able to predict the next token in the sequence by the tokens that precede it if we use a tokenwise splitting of Wolfram Language expressions. We used the following recurrent neural network architecture with two Gated Recurrent Unit (GRU). The structure of our network is shown below.

We did experiments with different parameters of the network. Here, it is presented the final version where we added dropout regularisation to increase the generalisation ability of the model. On the following image, the wrapper of the network is shown where CE is cross-entropy loss function which is the target of optimisation, SR is a sequence-rest layer and SM is a sequence-most layer which are used to preprocess the sequence of tokens.
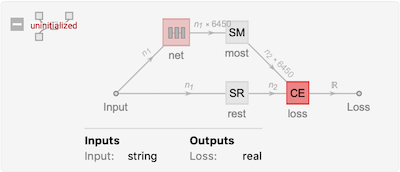
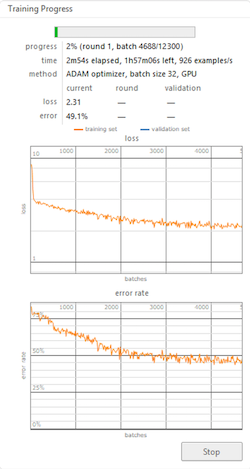
We used basic options of Wolfram Mathematica neural network trainer to train the network.
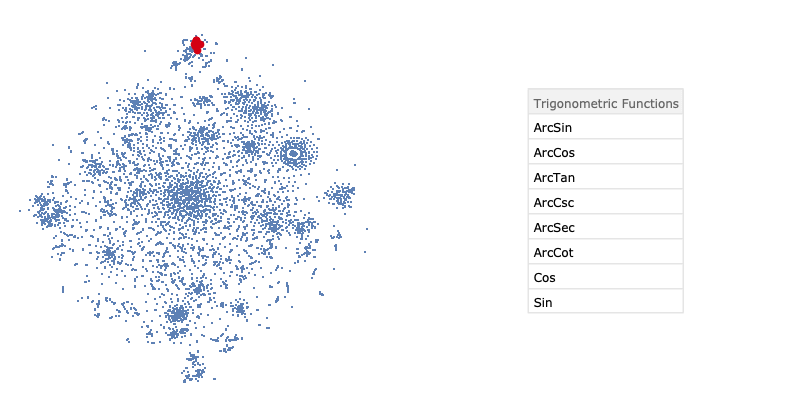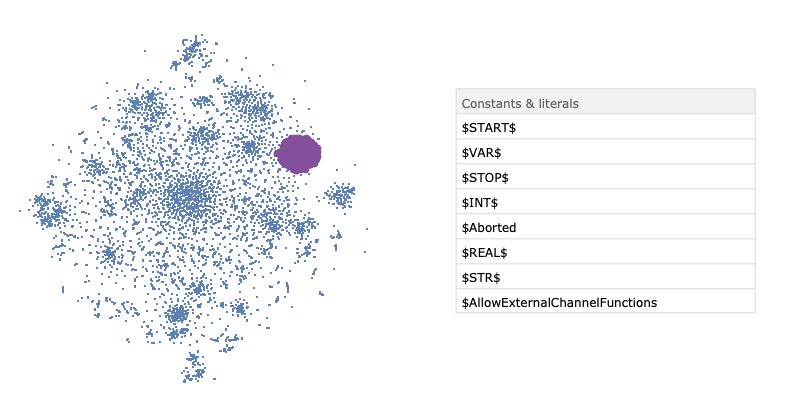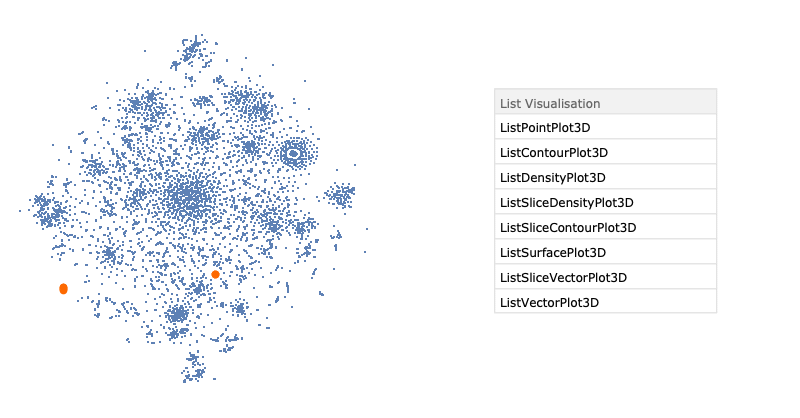
After training, we applied the dimensionality reduction technique t-SNE to visualise of embedding space. The result is presented below.
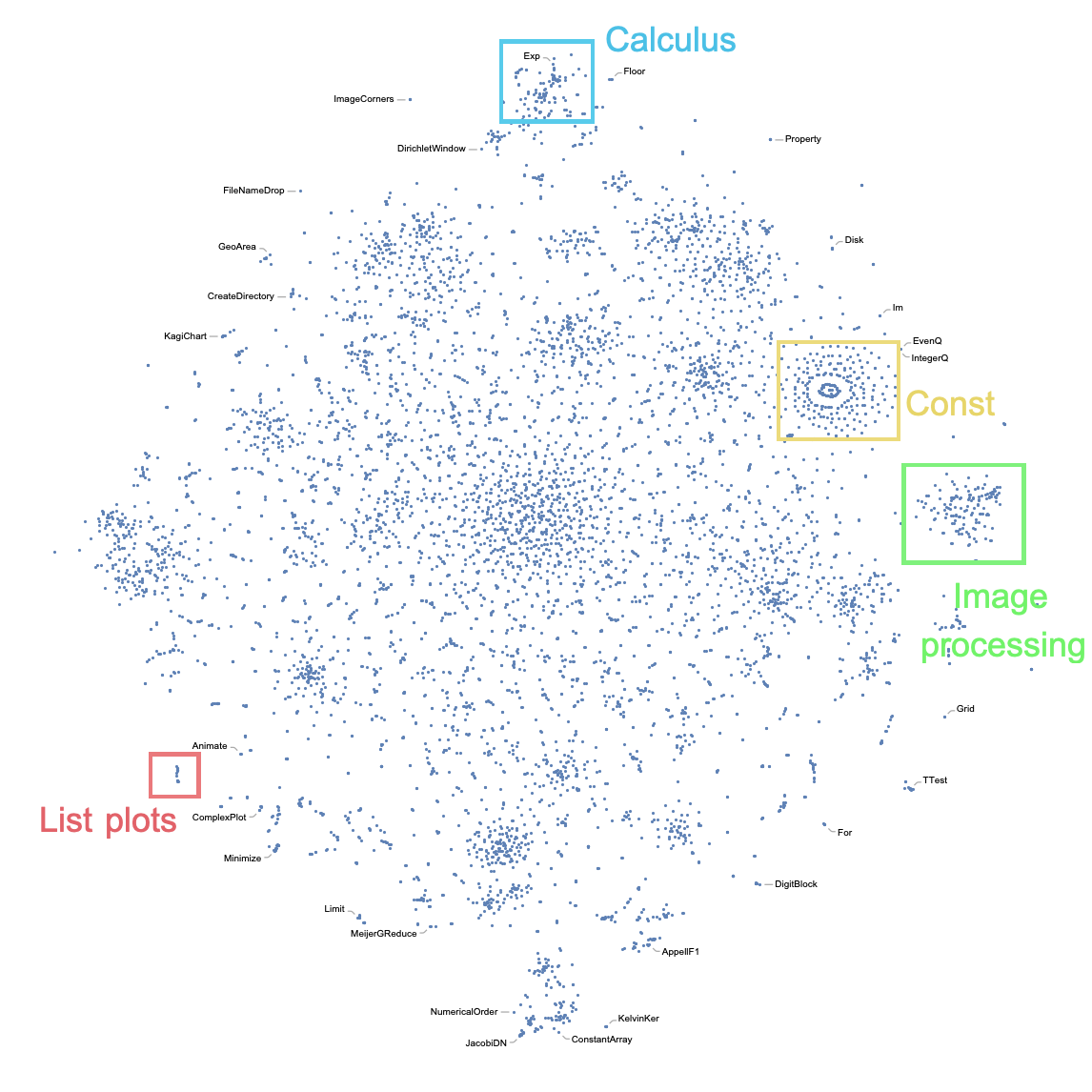
To summarise, we used a well-known task of language modelling to extract the semantic similarity of built-in Wolfram Language functions. Here, we trained an RNN with two GRU layers and dropout to predict the next symbol in the sequence of expression tokens. The restricted time in summer school allowed us to train only three different neural networks. As a result, we got an embedding vector space where the distance between the vector representing Wolfram Language functions and special symbols correspond to the semantic distance of them.
code2vec
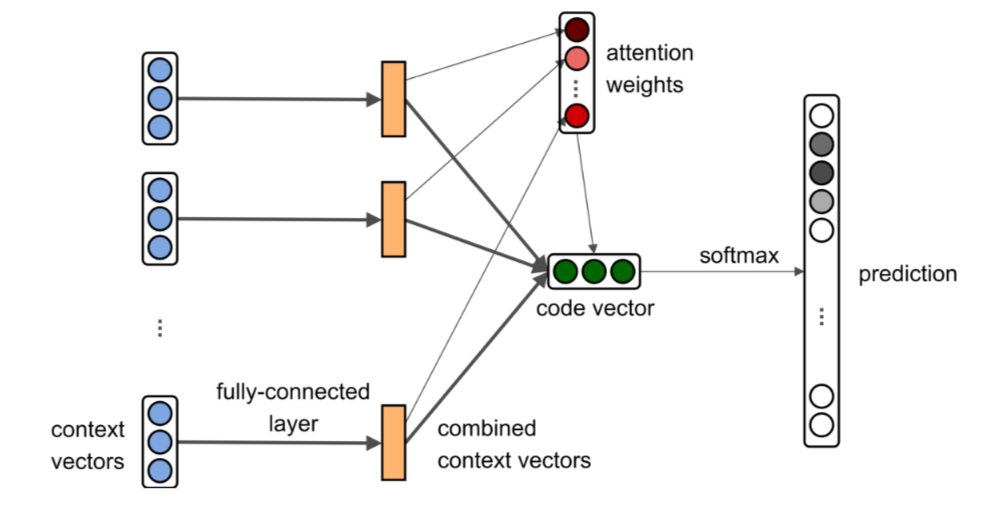
Another approach was suggested in the article "code2vec: learning distributed representations of code". The authors use a method-level granularity. According to their work, every method is represented as a bag of paths between terminal nodes in an abstract syntax tree. The formal explanation of the method can be found in the original article. If we apply this paths-based encoding to train network predicting names of methods it can be used to predict the name for methods based on the structure of them. The following picture is from the original paper where we can see the structure of the used attentional neural network.
For this approach, we implemented the paths-based encoding for Wolfram Language expressions. But in addition to the originally suggested paths, we also consider paths from the root to terminal nodes to be able to encode expressions with less than two terminal nodes. An example of an expression tree with highlighted paths is presented below.

Later, we realised that we did not have enough data and time to train this model so we postponed it for future research.
To try the state-of-the-art approach, we used code2vec which is presented in the article[13]. During Wolfram Summer School we implemented encoder which builds a paths-based representation of a Wolfram Language expression. Training an attentional neural network and exploration of the results is a topic of future works.
Conclusions
In our project, we tried to explore different forms of embeddings for Wolfram Language. For this purpose, we:
- gathered a lot of samples of code in Wolfram Language
- cleaned the samples and made them interpretable
- trained a couple of classical neural network architectures
- did experiments with a state-of-the-art method in source code embeddings
- got images of embedding vector space in 2D
Future work
During the project, we built a pipeline to start exploring embedding for Wolfram Language. There are loads of open questions about optimal neural network architecture and parameters which can be studied in the future. Also, there are other several approaches based on machine learning successfully applied to different program languages, which could be implemented for the language. See the following review. Finally, it is interesting to find how to use the symbolic structure of Wolfram Language to represent programs expressively for machine learning.
References
- Wikipedia: Halting problem
- Wikipedia: Machine learning
- Wikipedia: Neural network
- Wikipedia: One-hot
- Wikipedia: Language model
- Wikipedia: Recurrent neural network
- Wikipedia: Gated recurrent unit
- Wikipedia: Dropout
- Wikipedia: Cross entropy
- Wolfram: SequenceRestLayer
- Wolfram: SequenceMostLayer
- Wikipedia: T-distributed stochastic neighbor embedding
- arXiv: code2vec: Learning Distributed Representations of Code
- arXiv: A Literature Study of Embeddings on Source Code