I want to solve the followiwng system of equations:
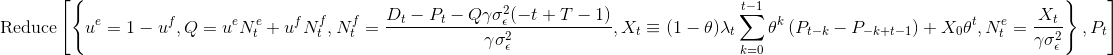
Reduce[{u^e == 1 - u^f, Q == u^e \!\(\*SubsuperscriptBox[\(N\),
\(t\), \(e\)]\) + u^f \!\(\*SubsuperscriptBox[\(N\), \(t\), \(f\)]\),
\!\( \*SubsuperscriptBox[\(N\), \(t\), \(f\)] == \*FractionBox[\(
\*SubscriptBox[\(D\), \(t\)] - \*SubscriptBox[\(P\), \(t\)] - Q\
\((\(-1\) - t + T)\)\ \*SubsuperscriptBox[\(\[Gamma]\[Sigma]\),
\(\[Epsilon]\), \(2\)]\), SubsuperscriptBox[\(\[Gamma]\[Sigma]\),
\(\[Epsilon]\), \(2\)]]\), Subscript[X, t] ==
\[Theta]^t Subscript[X,
0] + (1 - \[Theta]) Subscript[\[Lambda], t] \!\( \*UnderoverscriptBox[\(\[Sum]\), \(k = 0\), \(\(-1\) + t\)]\(
\(\*SuperscriptBox[\(\[Theta]\), \(k\)]\)[\(- \*SubscriptBox[\(P\),
\(\(-1\) - k + t\)]\) + \*SubscriptBox[\(P\), \(\(-k\) + t\)]]\)\),
\!\( \*SubsuperscriptBox[\(N\), \(t\), \(e\)] == \*FractionBox[
SubscriptBox[\(X\), \(t\)], SubsuperscriptBox[\(\[Gamma]\[Sigma]\),
\(\[Epsilon]\), \(2\)]]\)}, \ Subscript[P, t]]
Unfortunately, neither reduce nor solve work here. I get the error message: ". is not a quantified system of equations and inequalities." What does that mean?