Integrate[Sqrt[1 + 1/(-x^2 + 1)]*Exp[-(u - x)^2], {x, -1/2, 1/2}]
(* Returns an input,Mathematica dosen't know the answer.*)

When Mathematica returns the input as the output, it means that the calculation returned unevaluated. This often means that the function does not have the methods available to solve the problem symbolically, or it is mathematically impossible to obtain a symbolic solution (not all sums, integrals, or differential equations have symbolic solutions after all).

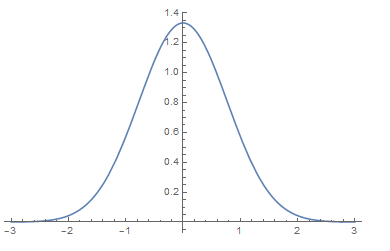
With numerics we able a plot solution:

g[u_?NumericQ] := NIntegrate[Sqrt[1 + 1/(-x^2 + 1)]*Exp[-(u - x)^2], {x, -1/2, 1/2}]
Plot[g[u], {u, -3, 3}]

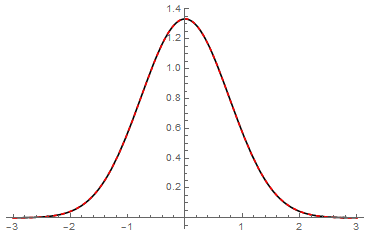
By using NonlinearModelFit command we can find a good approximate function:

data = Table[{u , g[u]}, {u, -3, 3, 1/10}] // N;
nlm = NonlinearModelFit[data, a + b*Exp[-c*u^2 + d], {a, b, c, d}, u] // Normal


(* -0.00114935 + 0.399547 E^(1.20727 - 0.846568 u^2) *)

Plot[{g[u], nlm}, {u, -3, 3}, PlotStyle -> {Black, {Dashed, Red}}]

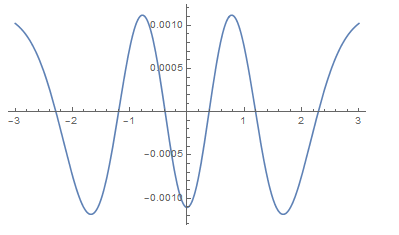
Plot[{g[u] - nlm}, {u, -3, 3}](*Residuals*)

Regards M.I.