Group Abstract

Message Boards

6.6K Views

2 Replies

0 Total Likes

View groups...

Follow this post

Share this post:

GROUPS:

Mathematics Mathematica

Posted 12 years ago

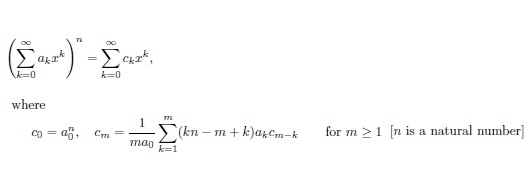
Is there anybody can help me to get an expansion for the following finite Power Sum? (Sum[(\[Beta]*x)^i/i!, {i, 0, m - 1}])^n As I know the infinite power sum can be expressed as follows but what about the case of finite power sum? Thanks for your support

POSTED BY: John G

2 Replies

Sort By:

Posted 12 years ago

I get the following result using Mathematica 9: In[1]:= (Sum[(\[Beta]*x)^i/i!, {i, 0, m - 1}])^n Out[1]= ((E^(x \[Beta]) Gamma[m, x \[Beta]])/Gamma[m])^n S M Blinder

POSTED BY: S M Blinder

Posted 12 years ago

Thanks for your reply, but I need to get a result in summation form, and Not in Gamma function.

POSTED BY: John G

Reply to this discussion

Reply Preview

Attachments

Remove Add a file to this post

Follow this discussion

or Discard

Feedback