Message Boards

6061 Views

2 Replies

0 Total Likes

View groups...

Follow this post

Share this post:

GROUPS:

Mathematics Mathematica

How to obtain the power series of finite power sum?

Posted 11 years ago

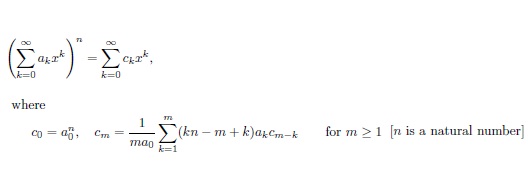
Is there anybody can help me to get an expansion for the following finite Power Sum? (Sum[(\[Beta]*x)^i/i!, {i, 0, m - 1}])^n As I know the infinite power sum can be expressed as follows but what about the case of finite power sum? Thanks for your support

POSTED BY: John G

2 Replies

Sort By:

Posted 11 years ago

I get the following result using Mathematica 9: In[1]:= (Sum[(\[Beta]*x)^i/i!, {i, 0, m - 1}])^n Out[1]= ((E^(x \[Beta]) Gamma[m, x \[Beta]])/Gamma[m])^n S M Blinder

POSTED BY: S M Blinder

Posted 11 years ago

Thanks for your reply, but I need to get a result in summation form, and Not in Gamma function.

POSTED BY: John G

Reply to this discussion

Reply Preview

Attachments

Remove Add a file to this post

Follow this discussion

or Discard

Feedback