You can complete the square to verify that you have a circle of radius $\sqrt{5}$ centered at (3,1).

x^2 + y^2 - 6 x - 2 y + 5 == (x - 3)^2 + (y - 1)^2 - 5 // Simplify
(* True *)

There are two solutions for $k$. You can use the GeometricScene functionality (new in v12) to create a nice looking scene based on geometric constraints. For example:

positivek = 
 RandomInstance[
  GeometricScene[{{o -> {0, 0}, a, b, 
     c -> {3, 1}}, {r -> Sqrt[5]}}, {circ = Circle[c, r], 
    EuclideanDistance[c, a] == EuclideanDistance[c, b], 
    EuclideanDistance[c, a] == r, 
    PlanarAngle[{a, c, b}] == 90 Degree , 
    GeometricAssertion[{o, a, b}, "Collinear"]}], RandomSeeding -> 1]
negativek = 
 RandomInstance[
  GeometricScene[{{o -> {0, 0}, a, b, 
     c -> {3, 1}}, {r -> Sqrt[5]}}, {circ = Circle[c, r], 
    EuclideanDistance[c, a] == EuclideanDistance[c, b], 
    EuclideanDistance[c, a] == r, 
    PlanarAngle[{a, c, b}] == 90 Degree , 
    GeometricAssertion[{o, a, b}, "Collinear"]}], RandomSeeding -> 4]

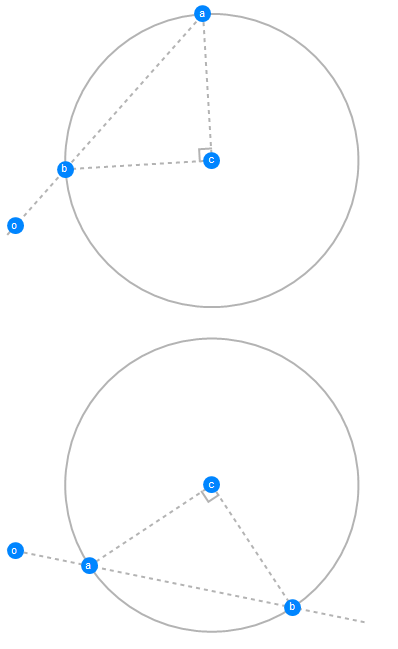
Now, you can calculate the slopes for the positive and negative case using the "Points" property of the scene.

a[[2]]/a[[1]] /. positivek["Points"] (* 1.127711849064953` *)
a[[2]]/a[[1]] /. negativek["Points"](* -0.20463492598802976` *)

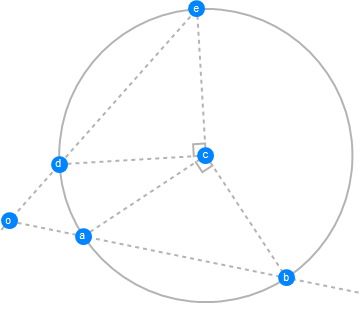
If desired, you can view the GeometricScene of both arcs on single plot.

RandomInstance[
 GeometricScene[{{o -> {0, 0}, a, b, c -> {3, 1}, d, 
    e}, {r -> Sqrt[5]}}, {circ = Circle[c, r], 
   EuclideanDistance[c, a] == EuclideanDistance[c, b] == 
    EuclideanDistance[c, d] == EuclideanDistance[c, e] == r, 
   PlanarAngle[{a, c, b}] == PlanarAngle[{d, c, e}] == 90 Degree, 
   GeometricAssertion[{o, a, b}, "Collinear"], 
   GeometricAssertion[{o, d, e}, "Collinear"], 
   GeometricAssertion[{a, d}, "Distinct"]}], RandomSeeding -> 2]

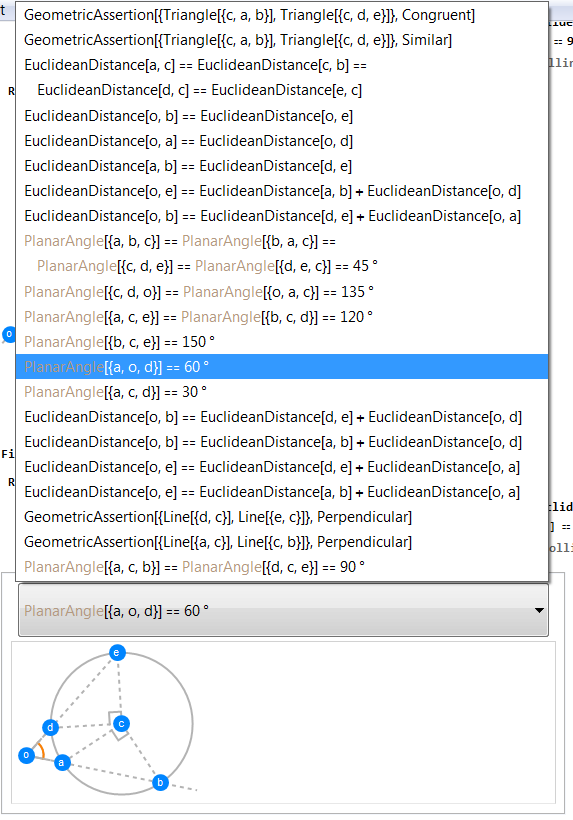
Finally, the FindGeometricConjectures function can help you discover other geometric relationships in the scene.

FindGeometricConjectures[
 RandomInstance[
  GeometricScene[{{o -> {0, 0}, a, b, c -> {3, 1}, d, 
     e}, {r -> Sqrt[5]}}, {circ = Circle[c, r], 
    EuclideanDistance[c, a] == EuclideanDistance[c, b] == 
     EuclideanDistance[c, d] == EuclideanDistance[c, e] == r, 
    PlanarAngle[{a, c, b}] == PlanarAngle[{d, c, e}] == 90 Degree, 
    GeometricAssertion[{o, a, b}, "Collinear"], 
    GeometricAssertion[{o, d, e}, "Collinear"], 
    GeometricAssertion[{a, d}, "Distinct"]}], RandomSeeding -> 2]]