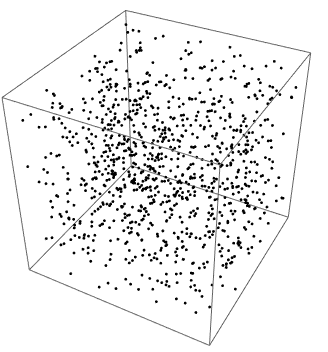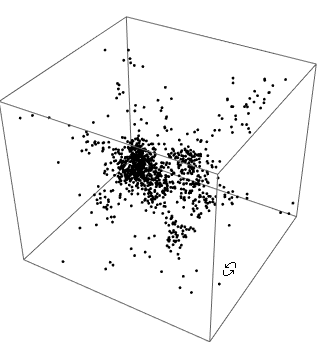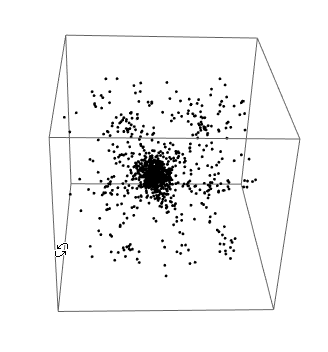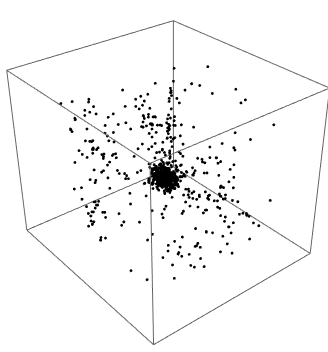
Just FYI - some related information. In the documentation there is an
interesting demo on the N-body simulation is a classic Newtonian problem. I think it was built on the
following tutorial which may give you some additional information.
Needs["OpenCLLink`"]
srcf = FileNameJoin[{$OpenCLLinkPath, "SupportFiles", "NBody.cl"}];
NBody = OpenCLFunctionLoad[{srcf},
"nbody_sim", {{"Float[4]", _, "Input"}, {"Float[4]", _, "Input"}, _Integer,
"Float", "Float", {"Local", "Float"}, {"Float[4]", _,
"Output"}, {"Float[4]", _, "Output"}}, 256];
numParticles = 1024;
deltaT = 0.05;
epsSqrt = 50.0;
pos = OpenCLMemoryLoad[RandomReal[512, {numParticles, 4}], "Float[4]"];
vel = OpenCLMemoryLoad[RandomReal[1, {numParticles, 4}], "Float[4]"];
newPos = OpenCLMemoryAllocate["Float[4]", {numParticles}];
newVel = OpenCLMemoryAllocate["Float[4]", {numParticles}];
NBody[pos, vel, numParticles, deltaT, epsSqrt, 256*4, newPos, newVel, 1024];
NBody[newPos, newVel, numParticles, deltaT, epsSqrt, 256*4, pos, vel, 1024];
Graphics3D[Point[
Dynamic[Refresh[
NBody[pos, vel, numParticles, deltaT, epsSqrt, 256*4, newPos, newVel,
1024];
NBody[newPos, newVel, numParticles, deltaT, epsSqrt, 256*4, pos, vel,
1024];
Take[#, 3] & /@ OpenCLMemoryGet[pos], UpdateInterval -> 0]]]]