Message Boards Message Boards

Tokyo 2020 Olympic and Paralympic Emblems

Kotaro Okazaki, FTI
Posted 5 years ago

The Olympic and Paralympic Games will be held in Tokyo in the summer of 2020. The emblems for them are shown below:

enter image description here

There is the explanation of these emblems on the official page.

Composed of three varieties of rectangular shapes, the design represents different countries, cultures and ways of thinking.It incorporates the message of "unity in diversity".It also expresses that the Olympic and Paralympic Games seek to promote diversity as a platform to connect the world.

And I have heard that someone who examined a rule in the emblem told that three rectangles that are inscribed in a small regular 12 polygon(dodecagon) is placed around a large regular 24 polygon(icositetragon). I would like to confirm this with Mathematica.

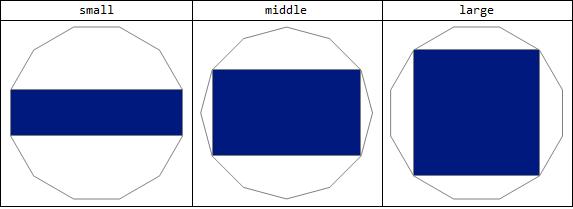
Three rectangles are below. 

eBlue = CMYKColor[1, .8, 0, .5]; (*emblem Blue*)
n = 12;
{rp, cp} = {RegularPolygon[n], CirclePoints[n]};
{rpx, cpx} = {RegularPolygon[{1, 0}, n], 
  CirclePoints[{1, 0}, n]}; Grid[{{"small", "middle", 
   "large"}, {Graphics[{EdgeForm[Directive[Thin, Gray]], White, rp, 
     eBlue, Rectangle[cp[[10]], cp[[4]]]}],
   Graphics[{EdgeForm[Directive[Thin, Gray]], White, rpx, eBlue, 
     Rectangle[cpx[[8]], cpx[[2]]]}],
   Graphics[{EdgeForm[Directive[Thin, Gray]], White, rp, eBlue, 
     Rectangle[cp[[11]], cp[[5]]]}]}}, Frame -> All]

enter image description here

Olympic Emblem

Define colors and rotation angles to be used after this.

oBlue = CMYKColor[1, .37, 0, 0];
oYellow = CMYKColor[0, .34, .91, 0];
oGreen = CMYKColor[1, 0, 1, 0];
oRed = CMYKColor[0, 0.94, 0.65, 0];

angle = Table[i*2 Pi/24, {i, 0, 24}];
  • STEP 1

Import an emblem and find the corners.

SetDirectory[NotebookDirectory[]];
emblem = Import["Tokyo_2020_Olympics_emblem.png"];
pad = 120;
i = ImagePad[emblem, pad, Transparent];
isize = (i // ImageDimensions);
pts = Sort@ImageCorners[i, 2, .001];
HighlightImage[i, pts]

enter image description here

Number the corners and display them.

ListPlot[pts -> ToString /@ Range[Length@pts], 
 LabelingFunction -> Above, Axes -> False, AspectRatio -> 1]

enter image description here

Find the radius and center of the regular 24 polygon that surrounds the emblem. Then, try composing the emblem and the regular 24 polygon.

radius24 = EuclideanDistance[pts[[1]], pts[[-1]]]/2;
c = (pts[[1]] + pts[[-1]])/2;
tmp = ImageCrop@
   Graphics[{EdgeForm[Directive[Thick, oBlue]], Transparent, 
     RegularPolygon[c, radius24, 24]},
    ImageSize -> isize - 2 pad];
rp24 = ImageResize[ImagePad[tmp, pad, White], isize];
ImageCompose[rp24, i]

enter image description here

  • STEP 2

Finds the radius and vertex of a regular dodecagon based on the size of a regular 24 polygon.

radius12 = EuclideanDistance[pts[[1]], pts[[4]]]/2;
p = CirclePoints[c, radius12, 12];

Defines a function that fits a rectangle inscribed in a regular dodecagon to a rectangle in the emblem.

fit[f1_, f2_, t1_, t2_, col_] := Module[{dis, deg, rec, rp12x, grp12},
  dis = t1 - f1;(*move*)
  deg = PlanarAngle[{0, 0} -> {f2 - f1, t2 - t1}, "Counterclockwise"]; 
  deg = First@Nearest[angle, deg, 1];(*Angle correction*)
  rec = Rotate[Rectangle[f1 + dis, f2 + dis], deg, t1];(*rotate*)
  rp12x = Rotate[RegularPolygon[c + dis, radius12, 12], deg, t1];
  grp12 = ImageResize[ImageCrop@Graphics[{
       PointSize[.005], Gray, Point[{0, 0}], 
       Point[isize],(*Set markers in the lower left and upper right*)           
       eBlue, rec,
       EdgeForm[Directive[Thick, col]], Transparent, rp12x 
       }, ImageSize -> isize], isize]
  ]

Place small and large rectangles.

s1 = fit[p[[10]], p[[4]], pts[[57]], pts[[70]], oYellow];
s2 = fit[p[[10]], p[[4]], pts[[34]], pts[[43]], oYellow];
s3 = fit[p[[10]], p[[4]], pts[[33]], pts[[49]], oYellow];
s4 = fit[p[[10]], p[[4]], pts[[3]], pts[[2]], oYellow];
s5 = fit[p[[10]], p[[4]], pts[[21]], pts[[4]], oYellow];
s6 = fit[p[[10]], p[[4]], pts[[27]], pts[[9]], oYellow];
l1 = fit[p[[11]], p[[5]], pts[[59]], pts[[69]], oGreen];
l2 = fit[p[[11]], p[[5]], pts[[36]], pts[[48]], oGreen];
l3 = fit[p[[11]], p[[5]], pts[[12]], pts[[18]], oGreen];

ImageMultiply[rp24, s1, s2, s3, s4, s5, s6, l1, l2, l3]

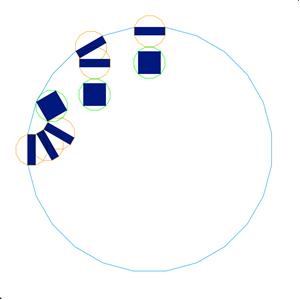
enter image description here

Place the remaining middle rectangles.

px = CirclePoints[c, {radius12, 0}, 12];
m1 = fit[px[[8]], px[[2]], pts[[49]], pts[[57]], oRed];
m2 = fit[px[[8]], px[[2]], pts[[48]], pts[[59]], oRed];
m3 = fit[px[[8]], px[[2]], pts[[18]], pts[[33]], oRed];
m4 = fit[px[[8]], px[[2]], pts[[38]], pts[[24]], oRed];
m5 = fit[px[[8]], px[[2]], pts[[20]], pts[[3]], oRed];
m6 = fit[px[[8]], px[[2]], pts[[21]], pts[[37]], oRed];

olym = ImageMultiply[rp24, s1, s2, s3, s4, s5, s6, l1, l2, l3, m1, m2,
   m3, m4, m5, m6]

enter image description here

Now that we have a third of the emplem, rotate it 120 and 240 degrees to complete the emplem.

ImageMultiply[olym,
 ImageRotate[olym, 2 Pi/3, Full, Masking -> Full, Padding -> White],
 ImageRotate[olym, 4 Pi/3, Full, Masking -> Full, Padding -> White]]

enter image description here

  • STEP 3

This emblem is made up of 45 rectangles of 15 types that are rotated based on 3 types of rectangles.

list = {s1, s2, s3, s4, s5, s6, l1, l2, l3, m1, m2, m3, m4, m5, m6};
imgs = Join[list, 
   ImageRotate[#, 2 Pi/3, Full, Masking -> Full, Padding -> White] & /@
     list, ImageRotate[#, 4 Pi/3, Full, Masking -> Full, 
      Padding -> White] & /@ list];
imgs = Join[list, 
   ImageRotate[#, 2 Pi/3, Masking -> Full, Padding -> White] & /@ 
    list, ImageRotate[#, 4 Pi/3, Masking -> Full, 
      Padding -> White] & /@ list];
olymparts = 
  ImageCrop@ImageCrop[#, 0.99*(# // ImageDimensions)] & /@ imgs;

c = ClusterClassify[olymparts, 15];
olymparts = GatherBy[olymparts, c];

Grid[Prepend[
  Map[ImageResize[#, 50] &, 
   olymparts[[{2, 12, 3, 4, 5, 1, 13, 6, 7, 14, 15, 10, 11, 9, 
      8}]], {2}], {"parts of Olympic emblem", SpanFromLeft, 
   SpanFromLeft}], Frame -> All]

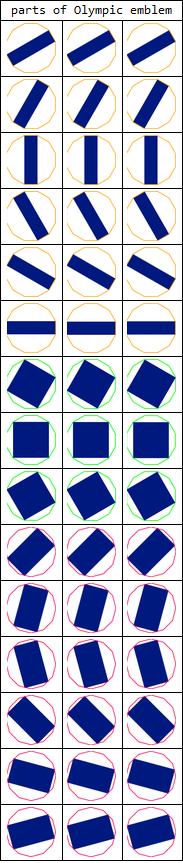
enter image description here

Paralympic Emblem

Repeat the same for the Paralympic emblem.

  • STEP 1 Import an emblem and find the corners.

    SetDirectory[NotebookDirectory[]];
emblem = Import["Tokyo_2020_Paralympics_emblem.png"];
pad = 120;
i = ImagePad[emblem, pad, Transparent];
isize = (i // ImageDimensions);
pts = Sort@ImageCorners[i, 2, .001];
HighlightImage[i, pts]

enter image description here

Number the corners and display them.

ListPlot[pts -> ToString /@ Range[Length@pts], 
 LabelingFunction -> Above, Axes -> False, AspectRatio -> 1]

enter image description here

Find the radius and center of the regular 24 polygon that surrounds the emblem. Then, try composing the emblem and the regular 24 polygon.

radius24 = EuclideanDistance[pts[[1]], pts[[-1]]]/2;
c = (pts[[1]] + pts[[-1]])/2;
tmp = ImageCrop@
   Graphics[{EdgeForm[Directive[Thick, oBlue]], Transparent, 
     RegularPolygon[c, radius24, 24]},
    ImageSize -> isize - 2 pad];
rp24 = ImageResize[ImagePad[tmp, pad, White], isize];
ImageCompose[rp24, i]

enter image description here

  • STEP 2

Finds the radius and vertex of a regular dodecagon based on the size of a regular 24 polygon.

radius24 = EuclideanDistance[pts[[1]], pts[[-1]]]/2;
c = (pts[[1]] + pts[[-1]])/2;
radius12 = EuclideanDistance[pts[[1]], pts[[4]]]/2;
p = CirclePoints[c, radius12, 12];
px = CirclePoints[c, {radius12, 0}, 12];

Place all rectangles.

s1 = fit[p[[10]], p[[4]], pts[[30]], pts[[39]], oYellow]; s2 = 
 fit[p[[10]], p[[4]], pts[[8]], pts[[13]], oYellow];
s3 = fit[p[[10]], p[[4]], pts[[3]], pts[[2]], oYellow];
s4 = fit[p[[10]], p[[4]], pts[[14]], pts[[5]], oYellow];
s5 = fit[p[[10]], p[[4]], pts[[25]], pts[[47]], oYellow];
s6 = fit[p[[10]], p[[4]], pts[[47]], pts[[61]], oYellow];
s7 = fit[p[[10]], p[[4]], pts[[53]], pts[[65]], oYellow];
s8 = fit[p[[10]], p[[4]], pts[[64]], pts[[66]], oYellow];(*later*)
s9 = fit[p[[10]], p[[4]], pts[[42]], pts[[59]], oYellow];
s10 = fit[p[[10]], p[[4]], pts[[57]], pts[[72]], oYellow];(*later*)

l1 = fit[p[[11]], p[[5]], pts[[19]], pts[[32]], oGreen];
l2 = fit[p[[11]], p[[5]], pts[[10]], pts[[23]], oGreen];
l3 = fit[p[[11]], p[[5]], pts[[22]], pts[[29]], oGreen];
l4 = fit[p[[11]], p[[5]], pts[[44]], pts[[51]], oGreen];
l5 = fit[p[[11]], p[[5]], pts[[63]], pts[[70]], oGreen]; (*later*)

m1 = fit[px[[8]], px[[2]], pts[[21]], pts[[30]], oRed];
m2 = fit[px[[8]], px[[2]], pts[[12]], pts[[8]], oRed];
m3 = fit[px[[8]], px[[2]], pts[[18]], pts[[3]], oRed];
m4 = fit[px[[8]], px[[2]], pts[[35]], pts[[14]], oRed];
m5 = fit[px[[8]], px[[2]], pts[[23]], pts[[46]], oRed];
m6 = fit[px[[8]], px[[2]], pts[[29]], pts[[42]], oRed];
m7 = fit[px[[8]], px[[2]], pts[[51]], pts[[57]], oRed];
m8 = fit[px[[8]], px[[2]], pts[[35]], pts[[53]], oRed];
m9 = fit[px[[8]], px[[2]], pts[[52]], pts[[64]], oRed];

para = ImageMultiply[rp24, s1, s2, s3, s4, s5, s6, s7, s9, l1, l2, l3,
   l4, m1, m2, m3, m4, m5, m6, m7, m8, m9]

enter image description here

Now that you have a half of the emblem, reflect it and add three rectangles in the middle to complete the emblem.

ImageMultiply[para, s8, s10, l5, ImageReflect[para, Left]]

enter image description here

  • STEP 3

This emblem is made up of 45 rectangles of 15 types that are rotated based on 3 types of rectangles.

list = {s1, s2, s3, s4, s5, s6, s7, s9, l1, l2, l3, l4, m1, m2, m3, 
   m4, m5, m6, m7, m8, m9};
paraimgs = Join[list, ImageReflect[#, Left] & /@ list, {s8, s10, l5}];
paraparts = 
  ImageCrop@ImageCrop[#, 0.99*(# // ImageDimensions)] & /@ paraimgs;
c = ClusterClassify[paraparts, 15];
paraparts = GatherBy[paraparts, c];

The Olympic emblem and the Paralympic emblem are made of the same 45 rectangles!

{Grid[Prepend[
   Map[ImageResize[#, 50] &, 
    olymparts[[{2, 12, 3, 4, 5, 1, 13, 6, 7, 14, 15, 10, 11, 9, 
      8}]], {2}], {"parts of Olympic emblem", SpanFromLeft, 
    SpanFromLeft}], Frame -> All],
 Grid[Prepend[
   Map[ImageResize[#, 50] &, paraparts, {2}], {"parts of Paralympic", 
    SpanFromLeft, SpanFromLeft}], Frame -> All]}

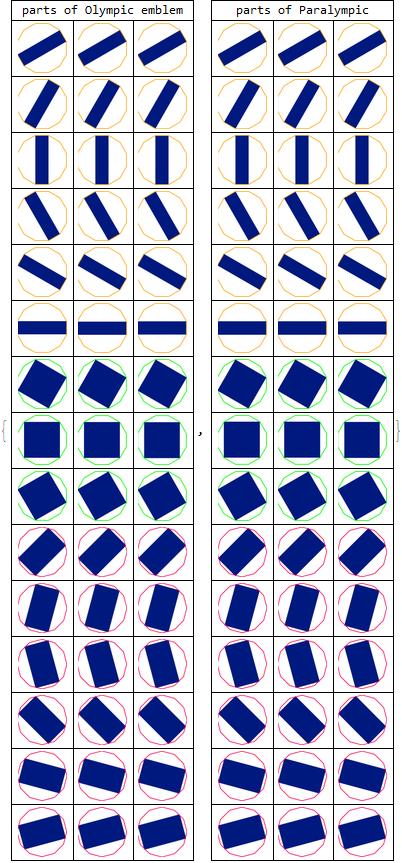
enter image description here

I am looking forward to Tokyo 2020. Before that, I will enjoy the Rugby World Cup 2019 in Japan this September.
POSTED BY: Kotaro Okazaki
4 Replies
Sort By:

On January 6, Tokyo 2020 Official Art Posters were published. The poster of Mr. Asao Tokolo who designed the Tokyo 2020 Olympic and Paralympic emblems is included in those. He said,

I created the designs as a tribute to the Tokyo 1964 designers, who relied on compasses and rulers for their creations, and by imagining what mediums would be employed by designers of the future.

I used his poster as a reference and have tried to make it in a different way than the one above.

enter image description here

R = 1;
line = 2 R Sin[11/12 Pi];
linecol := \!\(\*
TagBox[
StyleBox[
RowBox[{"RGBColor", "[", 
RowBox[{".9", ",", ".9", ",", ".9", ",", 
RowBox[{"RandomReal", "[", 
RowBox[{"{", 
RowBox[{"0.4", ",", "0.5"}], "}"}], "]"}]}], "]"}],
ShowSpecialCharacters->False,
ShowStringCharacters->True,
NumberMarks->True],
FullForm]\);
reccol = White;
backcol = CMYKColor[1, .8, 0, .5];(*emblem Blue*)
thick = Thickness[.001];
(* inside deformed 24 polygon *)
baseTriangle = {EdgeForm[Directive[thick, linecol]], FaceForm[None], 
   Triangle[{{0, 0}, {0, R}, R {Cos[Pi/3], Sin[Pi/3]}}]};
g1 = Table[Rotate[baseTriangle, i Pi/6, {0, 0}], {i, 0, 12}];
baseLine = {thick, linecol, Line[{{0, 0}, {0, R Cos[11 Pi/12]}}]};
g2 = Table[Rotate[baseLine, Pi/12 + i Pi/6, {0, 0}], {i, 0, 11}] ;
(* 3 rectangles *)
rectangle[theta_] := Module[{p0, p1, p2, p3, rhombus},
  p0 = {0, 0};
  p1 = line {Cos[theta], Sin[-theta]};
  p2 = line {2 Cos[theta], 0};
  p3 = line {Cos[theta], Sin[theta]};
  rhombus = {EdgeForm[Directive[thick, linecol]], FaceForm[None], 
    Polygon[{p0, p1, p2, p3}], linecol, Line[{p0, p2}], 
    Line[{p1, p3}], Line[{p0 + p1, p2 + p3}/2], 
    Line[{p1 + p2, p3 + p0}/2],
    PointSize[.008], Point[{p0, p1, p2, p3}]};
  {FaceForm[{reccol, Opacity[RandomReal[{0.2, 0.7}]]}], 
   Rectangle[p1/2, 1/2 (p2 + p3)], rhombus}
  ]
r1 := rectangle[Pi/4];  (*large*)
r2 := rectangle[Pi/6];  (*middle*)
r3 := rectangle[Pi/12];  (*small*)

g3 := {
  (*large rectangel*)
  Translate[Rotate[r1, Pi/2, {0, 0}], {0, R}],
  Translate[Rotate[r1, 0, {0, 0}], 
   line Cos[Pi/4] {-1, 
      0} + (R Cos[Pi/4] Cos[Pi/12] + line/2 Cos[Pi/4]) {-1, 1}],
  Translate[Rotate[r1, Pi/6, {0, 0}], 
   l1 = (R Cos[Pi/12] + line (1 + Sin[Pi/3])) {-Cos[Pi/12], 
      Sin[Pi/12]}],
  (*middle rectangel*)
  Translate[Rotate[r2, Pi/12, {0, 0}], {0, R}],
  Translate[Rotate[r2, -Pi/12, {0, 0}], {0, R + 2 line Sin[Pi/4]}],
  Translate[Rotate[r2, 11 Pi/12, {0, 0}], {0, R}],
  Translate[Rotate[r2, 13 Pi/12, {0, 0}], {0, R + 2 line Cos[Pi/4]}],
  Translate[Rotate[r2, 7 Pi/12, {0, 0}], {-R, 0}],
  Translate[
   Rotate[r2, 
    Pi/12, {0, 0}], {-R Cos[Pi/6] - line (Cos[Pi/4] + Cos[Pi/12]), 
    R Sin[Pi/3] + line Sin[Pi/12]}],
  (*small rectangel*)
  s1 := Translate[
    Rotate[r3, 0, {0, 0}], {0 - line Cos[Pi/12], 
     R + 2 line Sin[Pi/4] + line Sin[Pi/12]}],
  s1,
  Rotate[s1, Pi/6, {0, 0}],
  Translate[
   Rotate[r3, 0, {0, 0}], {0 - line (Cos[Pi/4] + 2 Cos[Pi/12]), 
    R + line Sin[Pi/4]}],
  s2 := Rotate[s1, Pi/2, {0, 0}],
  s2,
  Rotate[s2, Pi/6, l1],
  Rotate[s2, Pi/3, l1]};
g = Graphics[
   {g1, g2, g3,
    Rotate[g3, 2 Pi/3, {0, 0}],
    Rotate[g3, 4 Pi/3, {0, 0}]
    }, Background -> backcol, ImageSize -> 600];

ImageEffect[g, {"GaussianNoise", .1}]
POSTED BY: Kotaro Okazaki

Very nice and interesting - thanks for sharing!

Just a note: With a simple trick one can help the eye. Let corners be the corners of the emblem, then:

order = Last@FindShortestTour[corners];
Show[emblem, Graphics[{Opacity[.1], Red, EdgeForm@Directive[Thickness[.01], Red], Polygon[corners[[order]]]}]]

enter image description here

Outside the polygon there appear only rectangles of type "middle".
POSTED BY: Henrik Schachner

enter image description here - Congratulations! This post is now featured in our Staff Pick column as distinguished by a badge on your profile of a Featured Contributor! Thank you, keep it coming, and consider contributing your work to the The Notebook Archive!

POSTED BY: Moderation Team

Very neat! Thanks for sharing!
POSTED BY: Sander Huisman
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract