Message Boards Message Boards

0
|
8096 Views
|
5 Replies
|
8 Total Likes
View groups...
Share
Share this post:

Model a basic mechanical system: 1 spring with 2 hanging masses connected?

Mor Bo
Posted 5 years ago

Out of curiosity, I decided to build myself a model of a basic mechanical system, namely a spring fixed to a wall/ceiling, with two hanging masses (m1, m2) connected to each other with a rod. enter image description here Nothing particularly special, the parts swing up and down and come to a stand still (when adding damper that is)

However at a specific time, I would like to have the rod and second mass disappear or break off from the first mass, so I can plot/see the reaction and amplitude of remaining body...

However, I can't find such a block, or think of such a way to simulate a 'cut' in a fixed translation after a specified time. I had considered using a switch, however I can't connect the logic blocks to any of multibody ones.

How would one go about this?

POSTED BY: Mor Bo
5 Replies
Sort By:

One other thought I just had is maybe the reason my initialize to steady state does not work is that our initial position is too far from the steady solution. You can try moving the masses close and then try it.
POSTED BY: Neil Singer

Mor,

There is an option in Simulation Center under Tools>initialize>To Steady State but I could not get it to work for this model. You certainly would need to replace the detachable spring with a regular one.

One possibility is that you need to add some damping to the model so it eventually simulates to steady state. But even making the spring damped, the model takes a REALLY long time to settle (like never). You need to damp the pendulum effect to get the model to settle out. BUT, even trying this, I get errors from Kinsol (the kinematic solver) so I am not sure what the problem is.

Maybe @Ankit Naik has some insight on how to make initialization work with this model.

I'd like to know: Does the steady state initialization work on models without damping? Without damping there is a steady state but with any offset, the model will never get there. Why does Kinsol fail when I put damping in and get it to reach steady state?

Some other Ideas

  1. Alternatively, you can simulate the model to steady state yourself (if you add damping) and do initialize from Experiment, but this also does not seem to work with this model. I suspect a bug or incompatibility with the Multibody model??

  2. I suppose you can simulate to steady state and manually copy the steady state but I guess this will be problematic because you can't get the numbers exact so your system will not be consistent.

  3. I would try the same system without the Multibody components -- that will likely initialize and you can use those settings to initialize the Multibody simulation.

  4. You can extract the equations of motion of the system from SystemModeler to Mathematica and find the steady state solution on your own by setting all the derivatives to zero.

I hope this helps,

Regards,

Neil
POSTED BY: Neil Singer

Here is the model with the bar and mass flying off.

enter image description here

Attachments:
DetachableMasses.mo
POSTED BY: Neil Singer
Mor Bo
Mor Bo
Posted 5 years ago

Neil! Wow thanks for the help....or I guess doing the entire model for me. I never would have come up with the idea to use the line force.

Maybe you could answer another question for me.... When setting the initial conditions and the unstretched spring length to all the same, I would have expected the system to just simply hang, however it doesn't but bounces around. Is it possilbe to immediately have the system in stilstand from the get go?

Thanks again!
POSTED BY: Mor Bo

Mor,

The way to model a detaching mass is as a lineforce combined with a stiff spring representing the rigid translation. By editing a spring component, you can make the spring "give up" and apply no force when a boolean variable changes.

Here is an example system:

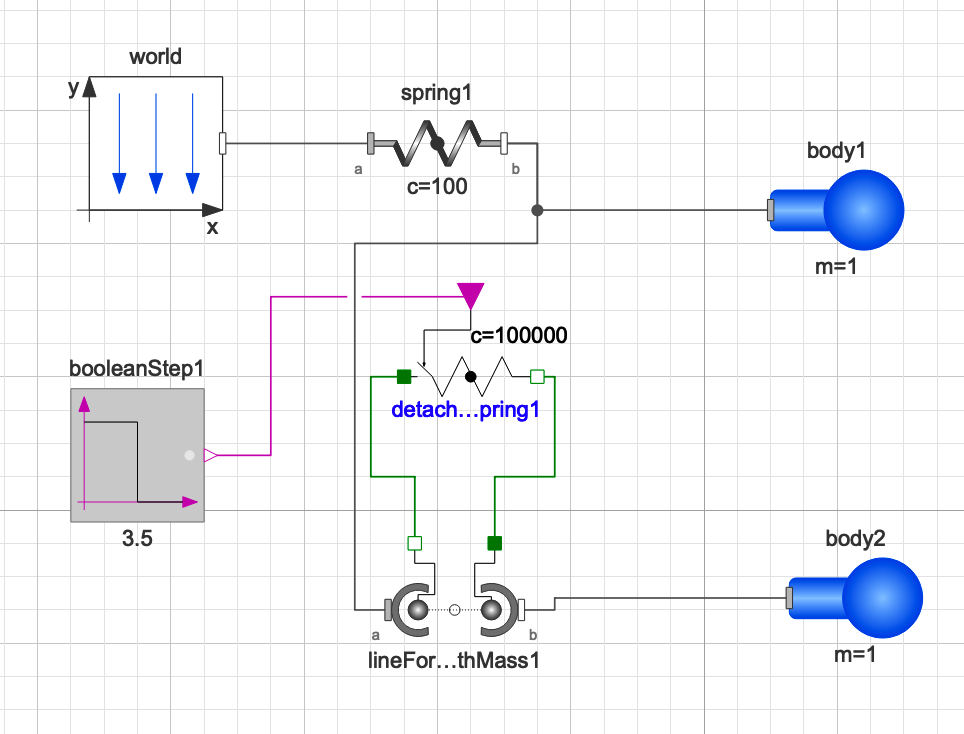
enter image description here

The detachable spring is coded:

model DetachableSpring
  import SI = Modelica.SIunits;
  extends Modelica.Mechanics.Translational.Interfaces.PartialCompliant;
  parameter SI.TranslationalSpringConstant c(final min = 0, start = 1) "spring constant ";
  parameter SI.Distance s_rel0 = 0 "unstretched spring length";
  Modelica.Blocks.Interfaces.BooleanInput attached annotation(Placement(visible = true, transformation(origin = {-100.0, 68.0}, extent = {{-20.0, -20.0}, {20.0, 20.0}}, rotation = 0), iconTransformation(origin = {0.0, 120.0}, extent = {{-20.0, -20.0}, {20.0, 20.0}}, rotation = -90)));
equation
  f = if attached then c * (s_rel - s_rel0) else 0;
end DetachableSpring;

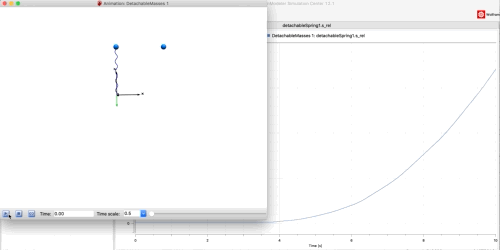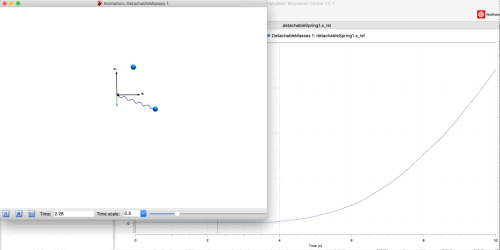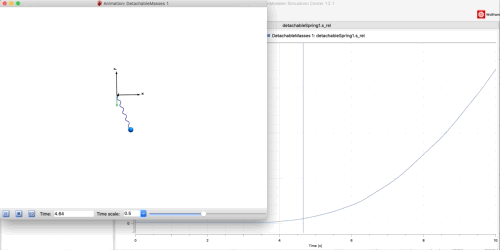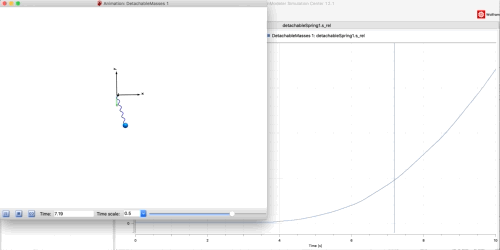
The simulation looks like this (note the distance between the masses is plotted in the background showing the release at 3.5 seconds.

The full model is attached.

enter image description here

Regards,

Neil

Attachments:
DetachableMasses.mo
POSTED BY: Neil Singer
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract