The integral of a Chebyshev series may be expressed as another Chebyshev series using the identities here supplemented with

Integrate[ChebyshevT[0, x], x] == ChebyshevT[1, x]

and

Integrate[ChebyshevT[1, x], x] == (ChebyshevT[2, x] + ChebyshevT[0, x])/4.

The Remes algorithm used by MiniMaxApproximation is notoriously slow, and polynomials represented by power series are notoriously ill-conditioned. For these problems, I like to use Chebyshev polynomials as a basis. It is common for a fitted Chebyshev series to yield almost as good a result as a minimax polynomial. It generally doesn't suffer from the "higher error at the ends" phenomenon. Rescale your independent variable so that its range is (-1,1) and then use ChebyshevT[n,x] with n equal 1, 2, 3, ... as your set of functions for LinearModelFit.

A good numerical library will have fast, accurate functions to calculate Chebyshev polynomials, so the results should transfer well to code in other languages.

For your function F[x], try using LinearModelFit on a set of points on the function. Note F[x] runs much faster with Real input values of high precision compared to fractional values.

pnts = Table[{x, F[x]}, {x, N[5/100, ndigits], N[1/4, ndigits], N[1/400, ndigits]}];

mons = NestList[(#*x) &, x, 20]; (* monomials for the polynomial fit *)

lm = LinearModelFit[pnts, mons, x];

ListPlot[lm["FitResiduals"],Filling->Axis,PlotRange->All];

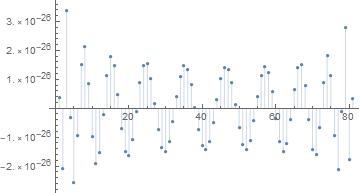
You can increase nDigits and the number of terms in the polynomial as needed to get the precision you need. I hope that you find this helpful.