I am aware of these problems, but I would prefer to obtain fitted polynomials using power basis, because I need to process them further (analytically integrate) in my program. Chebyshev or other basis would be less convenient from this point of view. I believe I should be able to get useful results using LinearModelFit, but I don't understand the technical problems described in my former message. I also do not find any relevant information about the error messages I obtain, on the web. So, perhaps someone can tell me what happens and how to successfully accomplish the calculations. Leslaw.

Thanks, it seems that this method indeed works much faster, and from my preliminary calculations I see that it may produce satisfactory results for my purposes. However, it is well known that least squares fits yield large residuals at the ends of the intervals, whereas minimax gives uniform residuals. Hence, least squares fits may not be optimal. In any case, I experience strange behavior of LinearModelFit. Although I specify the polynomial degree, I notice that the polynomials obtained are not necessarily of that order; the actual order is often smaller. Is this normal? Why this happens? Another problem is that in some cases I obtain error messages that some tensors are of incompatible shape, and the algorithm does not output a polynomial. For the attached code this happens with approx6, approx7 and some further ones. What I am doing wrong? Leslaw

Attachments:

icylw_fit.txt

For your function F[x], try using LinearModelFit on a set of points on the function. Note F[x] runs much faster with Real input values of high precision compared to fractional values.

pnts = Table[{x, F[x]}, {x, N[5/100, ndigits], N[1/4, ndigits], N[1/400, ndigits]}];

mons = NestList[(#*x) &, x, 12]; (* monomials for the polynomial fit *)

lm = LinearModelFit[pnts, mons, x];

ListPlot[lm["FitResiduals"],Filling->Axis,PlotRange->All];

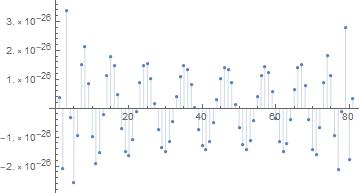
You can increase nDigits and the number of terms in the polynomial as needed to get the precision you need. I hope that you find this helpful.