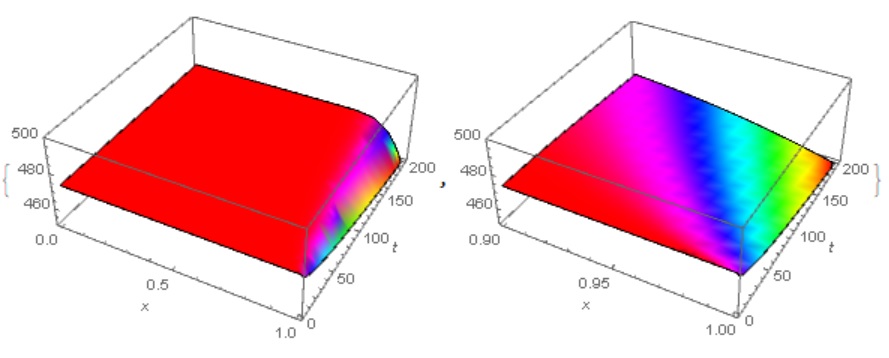
In this problem, it is necessary to coordinate the initial and boundary conditions, as well as use the solution method and increase the time interval to 200 for clarity.
eq = { 2423750 Derivative[0, 1][T][x, t] -
50 Derivative[2, 0][T][x, t] == 0};
bc = {Derivative[1, 0][T][0, t] == 0,
Derivative[1, 0][T][1,
t] == (5863/10 - 2*T[1, t]) (1 - Exp[-10 t])};
ic = T[x, 0] == 9463/20;
sol = NDSolveValue[{eq, ic, bc}, T, {x, 0, 1}, {t, 0, 200},
Method -> {"MethodOfLines",
"SpatialDiscretization" -> {"TensorProductGrid",
"MinPoints" -> 40, "MaxPoints" -> 100,
"DifferenceOrder" -> "Pseudospectral"}}, MaxSteps -> 10^6]
{Plot3D[Re[sol[x, t]], {x, 0., 1}, {t, 0, 200}, Mesh -> None,
ColorFunction -> Hue, PlotRange -> {450, 500},
AxesLabel -> Automatic],
Plot3D[Re[sol[x, t]], {x, 0.9, 1}, {t, 0, 200}, Mesh -> None,
ColorFunction -> Hue, PlotRange -> {450, 500},
AxesLabel -> Automatic]}