I'm trying to define a general procedure to fit experimental data like {{t1,x11,x21...}, {t2,x12,x22...}, {t3,x13,x23...}...} where ti is the time and xj are different observable magnitudes of the system.
I want to fit the data to a model given by a set of differential equations combining for that the NMinimize and NDSolve functions.
I have considered the following simplified problem.
1) My experimental data are just given by one observable magnitude as a function of time:
Xdat={{0.,0.},{2.5,0.274535},{5.,0.402493},{7.5,0.443142},{10.,0.434248},{12.5,0.39945},{15.,0.353193},{17.5,0.304003},{20.,0.256645},{22.5,0.213543},{25.,0.175702},{27.5,0.143293},{30.,0.116034},{32.5,0.0934173},{35.,0.0748496},{37.5,0.0597335},{40.,0.0475107},{42.5,0.0376818},{45.,0.0298143},{47.5,0.0235409},{50.,0.0185546},{52.5,0.0146022},{55.,0.0114765},{57.5,0.00900965},{60.,0.00706603},{62.5,0.00553691},{65.,0.00433544},{67.5,0.00339245},{70.,0.00265304},{72.5,0.00207375},{75.,0.00162023},{77.5,0.0012654},{80.,0.000987946},{82.5,0.000771099},{85.,0.000601692},{87.5,0.000469395},{90.,0.000366112},{92.5,0.000285506},{95.,0.000222611},{97.5,0.000173548},{100.,0.000135282}}
ListPlot[Xdata, Joined -> True, Frame -> True, PlotRange -> All]
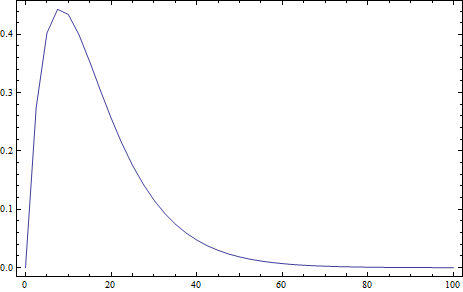
2) The next step I define the model given by a set of ODE's
model[p_List] := {x1'[t] == -p[[1]] x1[t],
x2'[t] == p[[1]] x1[t] - p[[2]] x2[t], x3'[t] == p[[2]] x2[t],
x1[0] == 1, x2[0] == 0, x3[0] == 0}
where the parameters p[[1]] and p[[2]] are the parameters to be optimized with NMinimize. I have decided to define the model in this way to allow the change of the name of the parameters.
3) The next step was the definition of the objective function where in this simple case reduces to the minimization of the sum of residuals, but in other problems involves several observable/state variables:
fun[data_, ode_] :=
Module[{nsol, x2teo, phi, yval, xval, tmax, param, nsolall},
{xval, yval} = Transpose[data];
tmax = Max[xval];
nsolall = NDSolve[ode, {x1[t], x2[t], x3[t]}, {t, 0, tmax}] ;
nsol = x2[t] /. nsolall[[1]];
x2teo = Evaluate[nsol] /. t -> xval;
phi = Total[(x2teo - yval)^2]
];
I need a general function like fun[] because I would like to try different models with the same data set without the requirement of writing a particular objective function for each model.
4) The function works properly with numerical arguments giving the value of the objective function at some point of the parameter space.
In[9]:= fun[Xdata, model[{0.01, 0.05}]]
Out[9]= 0.998479
ContourPlot[fun[Xdata, model[{x, y}]], {x, 0, 0.5}, {y, 0, 0.5}]
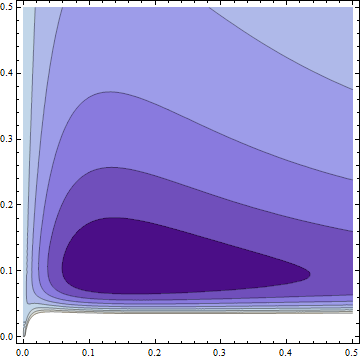
The function shows a well defined minima.
5) The last step is the use of NMinimize to obtain the best fit parameters. I have try to use the function as:
NMinimize[fun[Xdata, model[{p1, p2}]], {p1, p2}]
The function returns several errors on the evaluations basically saying that the function fun[] is not numerical.
I'm not sure if the problem is to understand how the NMinimize function works with symbols but I cannot fix this errors.
The use of Mathematica functions like FindFit[] or NonlinearModelFit[] are not feasible because are valid for problems where only there is one observable magnitude. The problem I'm trying to solve involve several state/observable variables and is not as simple as the precedent example.
I'll appreciate any comment and suggestion about the procedure or code that want to develop.
Regards,
Javier