Thank you, yehuda and Frank, your suggestion is very helpful. Actually, my question is going to find a optimal value w2 to maximize profit function:
Clear["`*"];
a = 10; b = 1; c = 2; v2 = 1; d2 = a - b*p2;
Q1[w2_] =
Maximize[{(p2*(a - b*p2) - (w2*(a - b*p2) - (v2*((a - b*p2))^2)/2)),
p2 >= a/b - (w2 - c)/(b*v2) && a/b > p2 > w2 > 0 && 2/b > v2 > 0 &&
b > 0}, {p2}]
Q3[w2_] =
Maximize[{(p2*d2 - (((w2)^2 - c^2)/(2*v2) + c*(d2 - (w2 - c)/v2))),
p2 <= a/b - (w2 - c)/(b*v2) && 0 < c < w2 < (a - b*c)*v2 + c &&
a/b > p2 > w2 > 0 && 2/b > v2 > 0 && b > 0}, {p2}]
By Q2, we can get optimal w2, Q3 will be the same. The optimal values are two piecewise functions, which are shown as follows:
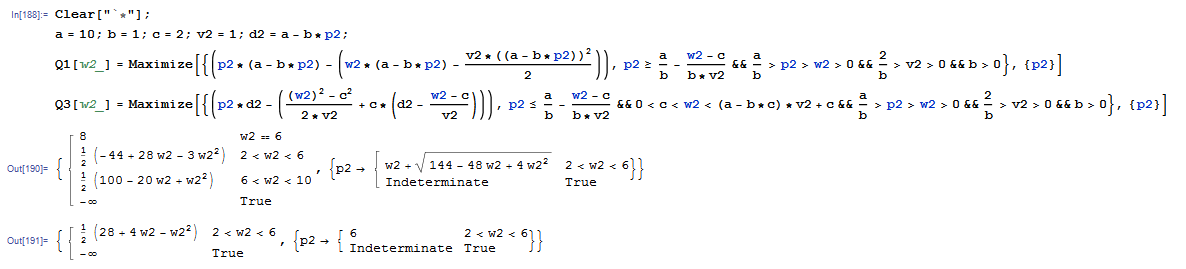
I want to compare the results to get the global optimal w2 and its profit, for instance, if global w2=6, its profit is 8. Of course, I can deal with this problem by hand calculation. However, what I am going to do involves many maximizing problem, so it would be better to use a simple command to calculate it. Additionally, in order to ensure that the solution is meaningful, w2 is greater than c and smaller than 6. Obviously, as to p2, when 2<w2<6, it is meaningful, w2 in other interval is meaningless.
another question is, if you change the assigment, for example, v2=1.5, mathematica doesn't work, the result is
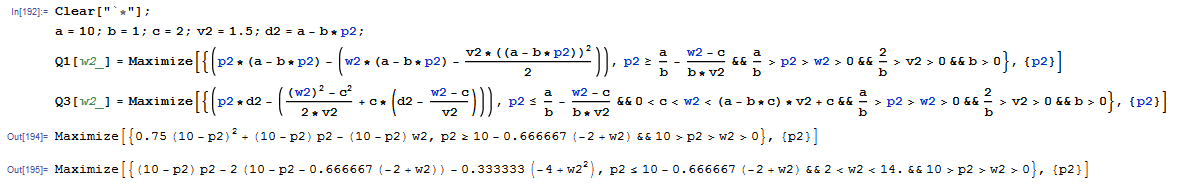
I tried several times and found that if your assigment is decimal number, it doesn't work, but it works for integers. Does it work only when the assigment is integer? What if I want to deal with decimal number? Thank you very much!