Introduction:

Here in this post, I demonstrate one form to visualize all possible ways of color the vertices of regular polygons, allowing rotations and reflections. The values (number) of possible options are known, but here I make them visual, in a function.

The following equations are the values for each regular polygon (3 sides to 10 sides), varying in the examples below; e.g.: the numbers to color vertices with 1 to 8 colors:

• For triangle (A000292-OEIS):

  Map[#*(# + 1)*(# + 2)/6 &, Range@8]
  

• For square (A002817-OEIS):

  Map[#*(# + 1)*(#^2 + # + 2)/8 &, Range@8]
  

• For pentagon (A060446-OEIS):

  Map[(#^5 + 5*#^3 + 4*#)/10 &, Range@8]
  

• For hexagon (A027670-OEIS):

  Map[#*(# + 1)*(#^4 - #^3 + 4*#^2 + 2)/12 &, Range@8]
  

• For heptagon (A060532-OEIS):

  Map[(#^7 + 7*#^4 + 6*#)/14 &, Range@8]
  

• For octagon (A060560-OEIS):

  Map[#*(# + 1)*(#^6 - #^5 + #^4 + 3*#^3 + 2*#^2 - 2*# + 4)/16 &, 
   Range@8]
  

• For 9-gon (A060561-OEIS):

  Map[(#^9 + 9*#^5 + 2*#^3 + 6*#)/18 &, Range@8]
  

• For 10-gon (A060562-OEIS):

  Map[(#^10 + 5*#^6 + 6*#^5 + 4*#^2 + 4*#)/20 &, Range@8]
  

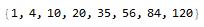
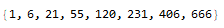
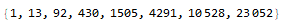
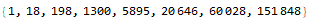
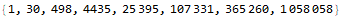
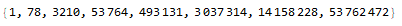
Code:

• Function 1 (case selector):

This first function serves to select the actual cases that are considered for each regular polygon in the demonstration:

vcases[a_, v_] := 
  Module[{rP, ap, no, du, in, e1, e2, ft, rangef, gt, 
    r1}, {no, du, in} = {Map[StringJoin[#] &, a], 
     Map[StringJoin@Table[#, 2] &, a], 
     Map[StringJoin[a[[#, Reverse@Range@v]]] &, Range@Length@a]}; {e1,
      e2} = {Map[StringCases[#, RegularExpression@no[[1]]] &, du], 
     Map[StringCases[#, RegularExpression@in[[1]]] &, du]};
   ft = Map[{Length@e1[[#]], 
        Length@e2[[#]]} /. {{2, 2} -> no[[#]], {2, 0} -> 
         no[[#]], {0, 2} -> {}, {0, 0} -> no[[#]], {2, 1} -> 
         no[[#]], {1, 2} -> {}, {1, 0} -> {}, {0, 1} -> {}, {1, 
          1} -> {}} &, Range@Length@du]; 
   rangef = Range@Length@DeleteCases[ft, {}]; 
   gt = Map[StringPartition[DeleteCases[ft, {}][[#]], 1] &, rangef]; 
   r1 = If[gt != {}, If[gt[[1]] == a[[1]], gt[[1]], {}], {}]; {rP = 
     DeleteCases[r1, {}], 
    ap = If[r1 != {}, DeleteCases[gt, r1], gt]}];

• Function 2 (number of ways):

The function with the number of ways to color the vertices (for a regular polygon and for a number of colors):

ways[v_, z_] := 
  v /. {3 -> (z*(z + 1)*(z + 2)/6), 4 -> (z*(z + 1)*(z^2 + z + 2)/8), 
    5 -> ((z^5 + 5*z^3 + 4*z)/10), 
    6 -> (z*(z + 1)*(z^4 - z^3 + 4*z^2 + 2)/12), 
    7 -> ((z^7 + 7*z^4 + 6*z)/14), 
    8 -> (z*(z + 1)*(z^6 - z^5 + z^4 + 3*z^3 + 2*z^2 - 2*z + 4)/16), 
    9 -> ((z^9 + 9*z^5 + 2*z^3 + 6*z)/18), 
    10 -> ((z^10 + 5*z^6 + 6*z^5 + 4*z^2 + 4*z)/20)};

• Function 3 (data generator and visualization):

This function below is the one that generates the data to be filtered by “function 1” as well as the end result that are the actual case visualizations:

RegularPolygonVertexColoring[v_, color_, OptionsPattern[]] := 
  Module[{rp, cp, ss, ss2, a, colorA, n, a1, b, diskp, 
    z = Length@color}, 
   colorA = color /. {color -> Take[Alphabet[], {1, z}]}; 
   Options[RegularPolygonVertexColoring] = {"Disk" -> GrayLevel[0.8], 
     "Size" -> 1, "Index" -> Off}; 
   diskp = {OptionValue["Disk"], Disk[{0, 0}, 2], EdgeForm[Thick], 
     White, rp, PointSize[0.13/Sqrt@OptionValue["Size"]]}; 
   If[z > 1, a = Tuples[colorA, v];
    n[x_] := {x}; a1 = a[[1]]; 
    ss = Last@
      Table[AppendTo[n[a1], 
        b = {a = vcases[a, v][[2]], vcases[a, v][[1]]}[[2]]], {ways[v,
           z] - 1}]; 
    ss2 = ss /. 
      Map[Take[Alphabet[], {1, z}][[#]] -> color[[#]] &, Range@z]; 
    Map[{rp, cp} = {RegularPolygon[v], CirclePoints[v]};
     Graphics[
       Join[diskp, {Point[cp, VertexColors -> #], 
         OptionValue["Index"] /. {Off -> {}, 
           On -> Text[
             Style[Flatten[Position[ss2, #]][[1]], 
              6*OptionValue["Size"], Bold, Black]]}}], 
       ImageSize -> 50*OptionValue["Size"]] &, 
     ss2], {Graphics[
      Join[diskp[[;; 4]], {RegularPolygon[v], color[[1]], diskp[[6]], 
        Point[CirclePoints[v]]}], 
      ImageSize -> 50*OptionValue["Size"]]}]];

Basics:

The common arguments of the function are as follows:

RegularPolygonVertexColoring[“polygon sides”,{“colors selection”}].

Regular polygons of 3 to 10 sides and 1 to 26 colors are parameters that can be used for the function. Some options are possible for the function (“Disk”, “Size”, “Index”) and are described below.

Examples and Options:

The disk behind the polygons is light gray as a default for the function (only for better visualization), but as an option we can change it to any color, for example, white as follows:

RegularPolygonVertexColoring[3,{Red,Blue},"Disk"->White].

Also, one can change the size (as a factor) of the graph with the optional "Size"; By default, the size factor is 1, but can be changed as follows, for example:

RegularPolygonVertexColoring[3,{Red, Blue},"Size"->2].

One can use indexes within polygons to identify them as an option for the function (“Index”->On), and works for 2 or more colors. Example:

RegularPolygonVertexColoring[3,{Red,Blue},"Index"->On].

Following are some examples of using the function on some regular polygons with variable color selection.

• All ways to color the vertices of a square with 5 colors:

  r1 = RegularPolygonVertexColoring[4, {Red, Blue, Green, Brown, Purple}]
  
  Length@r1
  

• All ways to color the vertices of a regular pentagon with 4 colors:

  r2 = RegularPolygonVertexColoring[5, {Red, Blue, Yellow, Orange}]
  
  Length@r2
  

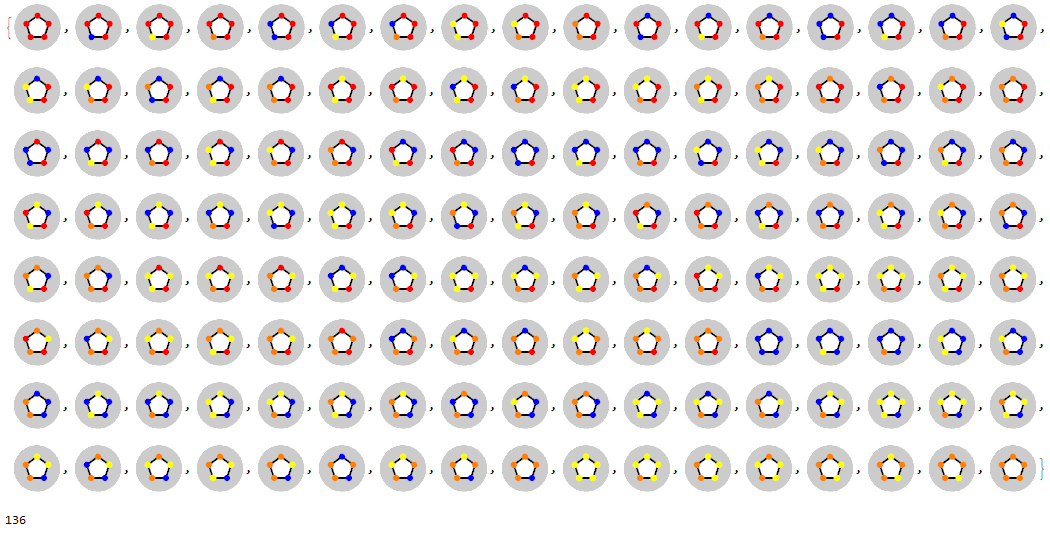
• All ways to color the vertices of a regular hexagon with 3 colors:

  r3 = RegularPolygonVertexColoring[6, {Pink, Cyan, Green}]
  
  Length@r3
  

• Example of using the function with the optional disc color change. Cyan “Disk”:

  RegularPolygonVertexColoring[3, {Red, Blue}, "Disk" -> Cyan]
  

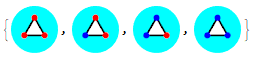
• Example of using the function with disk color change and size factor options. Green “Disk” and “Size” factor 5:

  RegularPolygonVertexColoring[10, {Purple}, "Size" -> 5, 
   "Disk" -> Green]
  

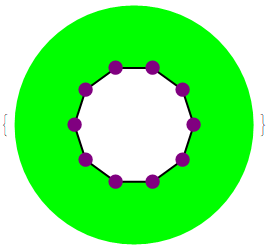
• All ways to color the vertices of regular polygons with 7, 8 and 9 sides with 2 colors, and with the options: “Size”->1.5 and “Index”->On:

  r4 = RegularPolygonVertexColoring[7, {Orange, Blue}, "Size" -> 1.5, 
    "Index" -> On]
  
  Length@r4
  
  r5 = RegularPolygonVertexColoring[8, {Yellow, Pink}, "Size" -> 1.5, 
    "Index" -> On]
  
  Length@r5
  
  r6 = RegularPolygonVertexColoring[9, {Red, Brown}, "Size" -> 1.5, 
    "Index" -> On]
  
  Length@r6
  

Example with many colors:

Defining a code to generate 14 different colors:

color14 = Map[ColorData[58, #] &, Range@14]

• All ways to color the vertices of a regular triangle using the 14 colors, “Size”->1.5 and “Index”->On:

  rx = RegularPolygonVertexColoring[3, color14, "Size" -> 1.5, 
    "Index" -> On]
  
  Length@rx
  

Notes:

The function of this post is designed to work with regular 3- to 10-sided polygons.

The function accepts up to 26 different colors simultaneously.

The greater the number of possible ways to color the polygon, the longer the time for evaluation.

Links (OEIS):

A000292 (N. J. A. Sloane)

https://oeis.org/A000292

A002817 (N. J. A. Sloane)

https://oeis.org/A002817

A060446 (N. J. A. Sloane)

https://oeis.org/A060446

A027670 (Alford Arnold)

https://oeis.org/A027670

A060532 (N. J. A. Sloane)

https://oeis.org/A060532

A060560 (N. J. A. Sloane)

https://oeis.org/A060560

A060561 (N. J. A. Sloane)

https://oeis.org/A060561

A060562 (N. J. A. Sloane)

https://oeis.org/A060562

Thanks.