Chinese article is published at https://mp.weixin.qq.com/s/yH2UpAWKIlywIhhw7tNzbQ
The exhaustive method can solve many problems. When the data size becomes larger, some optimization techniques are needed. Pruning is a common method. Exhaustion + pruning is a staple of the backtrack approach.
Handling such problems in Mathematica is very succinct. Commonly used is to arrange combination functions (Tuples, Permutations, Subsets, etc.) with Select, or use list operations to iterate, often two or three lines can solve the problem. However, there are also disadvantages. These permutation and combination functions generate a large list at one time and are not lazy evaluation. The data size is large or even out of memory, and the speed is also not efficient.
If you want to change the way you write, you will naturally think of using (multiple) loops or recursion. The efficiency of loops in Mathematica is not high, but it can be greatly accelerated with Compile. Compared to recursion, multiple loops are actually easier to be optimized by the compiler. In most programming languages, loops with many layers are nested in If layers, which is cumbersome to write, looks really impressive, but has poor scalability. So we need to avoid this. However, Mathematica has features such as "data is code, code is data, everything is expression" and good at symbolic calculation. We can easily perform meta-programming by writing codes to generate codes dynamically, and then compile. And thus speeding up the program, sometimes it is closed to the speed of the C language.
Sudoku Game

Sudoku is a mathematical logic game. The game consists of 9×9 grids. Players need to infer the numbers of other grids according to the numbers provided by the grid. They need to meet every row, column, and every thick line (3×3). The numbers are all 1 - 9, not repeated. This kind of game only needs logical thinking ability, and has nothing to do with digital operations. Although the game is simple, the numbers provided are ever-changing, so many educators believe that Sudoku is a good way to exercise youths' brains.
There are many ways to solve Sudoku. At present, the relevant Mathematica program found on the Internet could solve all solutions is often slow. Some faster programs can only get one solution.The following method is simple and rough which can get all the solutions, and the speed is also OK. It is not difficult to change to return only one solution, and can be further compiled into C code to accelerate.
- Enter the Sudoku matrix and replace 0 (blank) with the symbol variable.

N queens problem
The Eight Queens problem is an old and famous problem and is a typical case of backtracking algorithms. Place eight queens on 8×8 square chess so that they can't attack each other, that is, any two queens can't be in the same row, the same column or the same diagonal line. How many placement are there? The eight queens problem can be expanded to a more general n queen placement problem: the size of the board becomes n×n, and the number of queens becomes n.
If you pursue succinct, you can get it in one line of code. However, as the number of queens increases, when n=12, the memory of the normal computer is not enough.
Select[Permutations[v=Range@8],And@@Unequal@@@{#+v,#-v}&]//Length
Output:
92
Using an iterative version, when n=12, it takes 5 seconds, which is better than before, but it is not fast enough.
With[{n=12},
Nest[Join@@Table[Append[a,b],{a,#},
{b,With[{t=Range[Length[a],1,-1]},Complement[Range[n],a-t,a,a+t]]}]&,
{{}},n]]//Length//AbsoluteTiming
Output:
{5.04642, 14200}
With a multi-loop pruning version, when n=15, it takes only 3.6 seconds. Taking into account the symmetry reduction, some calculations take 2.4 seconds. For the sake of simplicity, only counting are considered here, and no specific solutions are collected. If you want to collect all the solutions, it takes only 4 seconds to use the Internal`Bag.
n = 15;
cf = With[{X = Symbol["x" <> ToString[#]] &},
Table[{X[j + 1],
If[Or @@ Table[X[j] == X[j - i] || Abs[X[j] - X[j - i]] == i, {i, j - 1}] /.
f : _Or :> Sort[f],
0, Evaluate@If[j < n, n, 1]]}, {j, n}
]
] /. {iter__} :>
Compile[{{x1, _Integer}},
Module[{cnt = 0}, Do[cnt++, iter]; cnt],
CompilationTarget -> "C", RuntimeOptions -> "Speed", RuntimeAttributes -> {Listable}
];
Total@cf@Range[n] // AbsoluteTiming
2 Total@Most[#] + If[OddQ[n], Last[#], 0] &@cf@Range[n/2 + 1] // AbsoluteTiming
Output:
{3.66029, 2279184}
{2.41061, 2279184}
As a comparison, two C language example programs on Wikipedia when n=15, take more than 3.7 seconds, using bits operation optimization version took 1.1 seconds, and the GCC compiler used by the C code opened the O3 optimization.
Fourth-order magic square
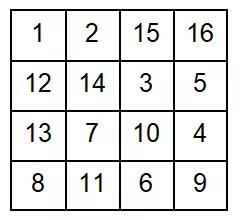
Fill the 4×4 squares with the numbers 1~16 so that the sum of the rows, columns, and the two diagonals are equal. When such a feature is satisfied, it is called: fourth-order magic square.
The general nature of the magic square is: the sum of each line of the magic square, the sum of each column, and the sum of the two diagonals are equal, which is equal to the Magic constant (the fourth-order Magic constant is 34).
Solve all fourth-order magic squares, use the full-arranged search space is too large, and there are 16!=2.09228*10^13 different situations for 16 numbers. According to the nature of the magic square, you can solve the following indefinite equations first, and then traverse the 7 variables, thus reducing the combination to A(16,7) = 16! / 9! = 57657600, which greatly reduces the search volume. 
There is a magic function in MATLAB, which can easily generate magic square, but can only generate a single. To generate all the fourth-order magic square, Matlab's father Cleve Moler once wrote a related blog post and shared the code. And a related paper: An Eficient Algorithm for Constructing all Magic Aquares of Order Four is also implemented by using MATLAB.
For the simplicity, the code is slightly modified to count only the number. In MATLAB R2019a, it took about 10 seconds to use parallel computing (the first time you start the parallel toolbox, you have to wait, and the timing has already been started). The corresponding Mathematica code is 4.4 seconds. 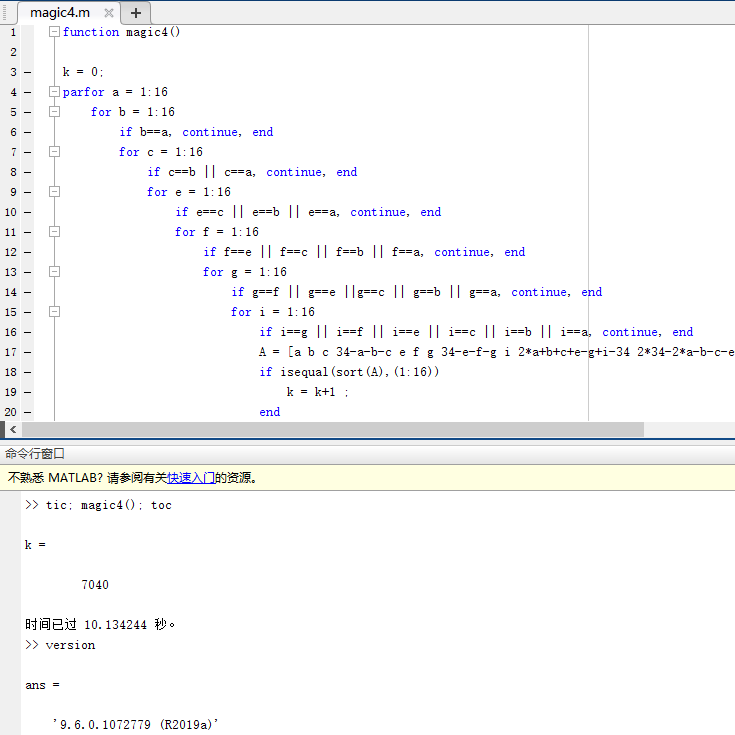
Clear[cf];
cf = Compile[{{i1, _Integer}},
Module[{A, k = 0},
Do[
If[Or[i7 == i6, i7 == i5, i7 == i4, i7 == i3, i7 == i2, i7 == i1], Continue[]];
A = {i1, i2, i3, 34 - i1 - i2 - i3, i4, i5, i6, 34 - i4 - i5 - i6, i7, -34 + 2 i1 + i2 + i3 + i4 - i6 + i7, 68 - 2 i1 - i2 - i3 - i4 - i5 - i7, i5 + i6 - i7,
34 - i1 - i4 - i7, 68 - 2 i1 - 2 i2 - i3 - i4 - i5 + i6 - i7, -34 + 2 i1 + i2 + i4 + i5 - i6 + i7, -34 + i1 + i2 + i3 + i4 + i7};
If[Sort@A == Range[16], k++],
{i2, 16},
{i3, If[i2 == i1, 0, 16]},
{i4, If[Or[i3 == i2, i3 == i1], 0, 16]},
{i5, If[Or[i4 == i3, i4 == i2, i4 == i1], 0, 16]},
{i6, If[Or[i5 == i4, i5 == i3, i5 == i2, i5 == i1], 0, 16]},
{i7, If[Or[i6 == i5, i6 == i4, i6 == i3, i6 == i2, i6 == i1], 0, 16]}];
k],
CompilationTarget -> "C", RuntimeOptions -> "Speed", RuntimeAttributes -> {Listable}];
Total@cf[Range[16]] // AbsoluteTiming
Output:
{4.38459, 7040}
After a better pruning, it takes less than 0.1 second.
Clear[cf];
cf = Module[{A, F, cond, iter},
A = {i1, i2, i3, 34 - i1 - i2 - i3, i4, i5, i6, 34 - i4 - i5 - i6, i7, -34 + 2 i1 + i2 + i3 + i4 - i6 + i7, 68 - 2 i1 - i2 - i3 - i4 - i5 - i7, i5 + i6 - i7, 34 - i1 - i4 - i7, 68 - 2 i1 - 2 i2 - i3 - i4 - i5 + i6 - i7, -34 + 2 i1 + i2 + i4 + i5 - i6 + i7, -34 + i1 + i2 + i3 + i4 + i7};
F = Symbol["i" <> ToString[#]] &;
cond = And @@ Thread[1 <= Complement[A, {i1, i2, i3, i4, i5, i6, i7}] <= 16] &&
Unequal @@ A // Not // LogicalExpand // Simplify;
Print[TableForm[
iter = Table[{F[n + 1],
If[Select[cond, F[n] == Last@Sort@Cases[#, _Symbol, -1] &], 0,
Evaluate@If[n < 7, 16, 1]]}, {n, 7}]]];
Compile[{{i1, _Integer}},
Module[{B = Internal`Bag[Rest@{0}]},
Do[Internal`StuffBag[B, #, 1], ##2];
Internal`BagPart[B, All]~Partition~4~Partition~4
],
CompilationTarget -> "C", RuntimeOptions -> "Speed", RuntimeAttributes -> {Listable}
] &[A, Sequence @@ iter]
];
Length[res = Join @@ cf[Range[16]]] // AbsoluteTiming
Output:
{0.0308292, 7040}
A Notebook for this post below.
 Attachments:
Attachments: