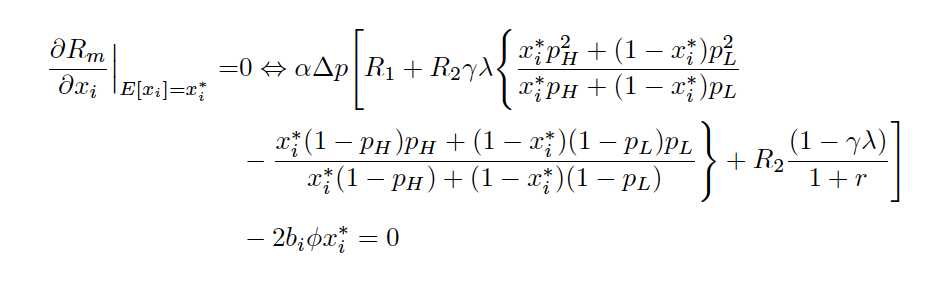Hi,
I have partially differentiated an equation w.r.t. x, see picture below, and want to isolate x in the equation to solve for a local maximum. This equation is part of my master's thesis and quite crucial. I know that, if rewritten, it will be cubic in x, thus, there can be at least three different solutions. However, at this moment, I am not able to obtain any solutions using Mathematica. Can you help me?
Attached there is a picture of the equation as it looks in the paper and also a picture of how I've written it into Mathematica.
Ideally, I would like to simplify it and find values of x that solves the equation.
I hope you can help.