Introduction:

(My questions are at the end of the post).

To work with lists of 1 billion significant digits of a number, one option is to use NumericArray[], specifically with the option “UnsignedInteger8”, so that each digit will occupy only 1 Byte instead of 8 Bytes, ie the consumption memory will be reduced by a factor of 8.

Below is exemplified the use of NumericArray[] (new and experimental - v.12), both digits are generated with RealDigits[] and the number of Bytes are counted:

ByteCount@RealDigits[Pi, 10, 1000][[1]]

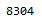
ByteCount@
 NumericArray[RealDigits[Pi, 10, 1000][[1]], "UnsignedInteger8"]

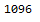
Examples with one billion digits:

Below are some examples with mathematical constants with one billion digits, in the case of Pi the time required to evaluate on my machine was about 35 minutes, but for other constants the time was varied, for: E, GoldenRatio, Sqrt2 the time was shorter, in descending order, while for EulerGamma I aborted the operation after about 5 hours. Note that the size of the operation is 10^9 Bytes, or 1 Gigabyte, but if not done this way, with NumericArray, would probably crash the system (+8Gb), at least on my machine.

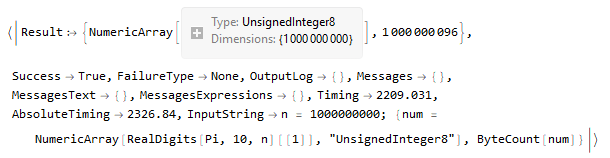
• Pi:

  EvaluationData[n = 1000000000;
   {num = NumericArray[RealDigits[Pi, 10, n][[1]], "UnsignedInteger8"], 
    ByteCount@num}]
  

Counting the digits for each type, not in appearance order but in numerical order, I used Table[] and Lookup[] in Counts[]:

counts = Table[{i, Lookup[Counts@(num // Normal), i]}, {i, 0, 9}]

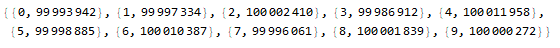
Testing the result with Part[]:

num[[;; 10]] // Normal

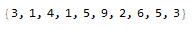
num[[857897882 ;; 857897899]] // Normal

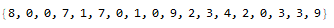
num[[1000000000]]

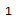
Note that above the significant billionth digit (taking into account the "3" on the left) of Pi is "1" and is different from the billionth digit of Pi, which is "9". All values can be checked by downloading some constants with billion digits from this site, and can be by torrent (about 10 Gigabytes). Below are the result of some more numbers with one billion digits:

• E:

• GoldenRatio:

• Sqrt2:

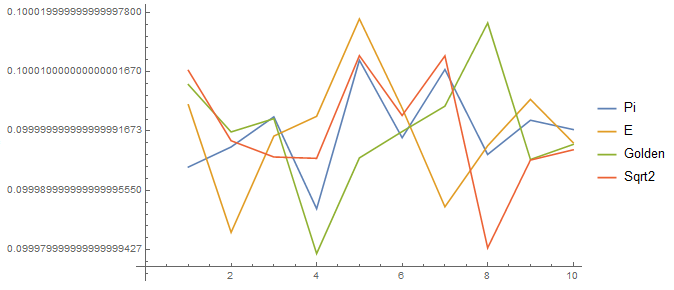
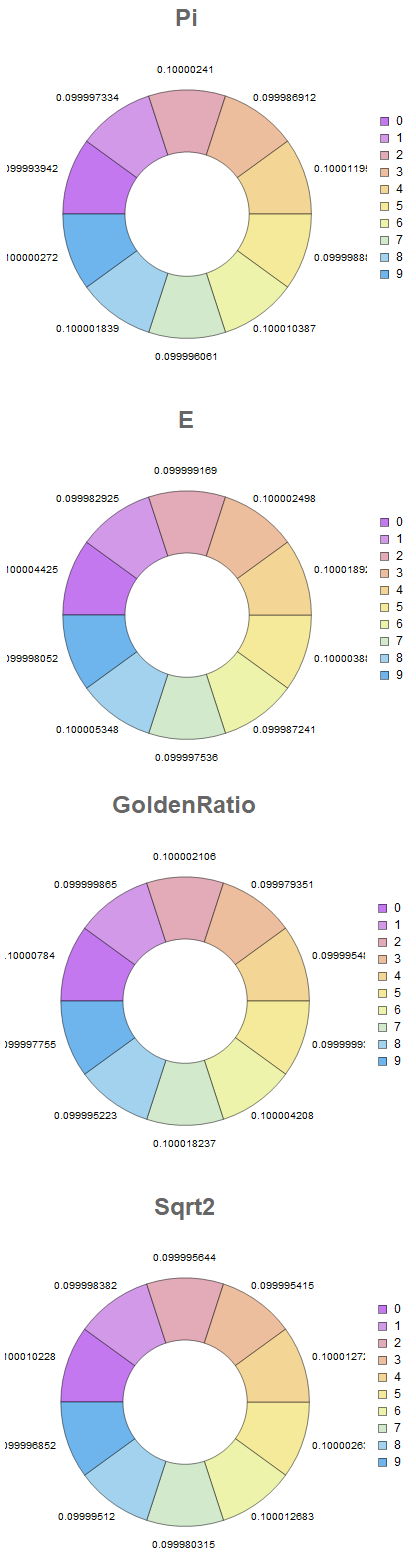
List and graph of results:

• List:

  cPi = {{0, 99993942}, {1, 99997334}, {2, 100002410}, {3, 
      99986912}, {4, 100011958}, {5, 99998885}, {6, 100010387}, {7, 
      99996061}, {8, 100001839}, {9, 100000272}};
  
  cE = {{0, 100004425}, {1, 99982925}, {2, 99999169}, {3, 
      100002498}, {4, 100018922}, {5, 100003884}, {6, 99987241}, {7, 
      99997536}, {8, 100005348}, {9, 99998052}};
  
  cGolden = {{0, 100007840}, {1, 99999865}, {2, 100002106}, {3, 
      99979351}, {4, 99995481}, {5, 99999934}, {6, 100004208}, {7, 
      100018237}, {8, 99995223}, {9, 99997755}};
  
  cSqrt2 = {{0, 100010228}, {1, 99998382}, {2, 99995644}, {3, 
      99995415}, {4, 100012725}, {5, 100002636}, {6, 100012683}, {7, 
      99980315}, {8, 99995120}, {9, 99996852}};
  

• Graph (%/100):

  c1 = Table[N[cPi[[i, 2]]/10^9], {i, 1, 10}]; c2 = 
   Table[N[cE[[i, 2]]/10^9], {i, 1, 10}]; c3 = 
   Table[N[cGolden[[i, 2]]/10^9], {i, 1, 10}]; c4 = 
   Table[N[cSqrt2[[i, 2]]/10^9], {i, 1, 10}];
  ListLinePlot[{c1, c2, c3, c4}, 
   PlotLegends -> {"Pi", "E", "Golden", "Sqrt2"}, ImageSize -> Large]
  Do[Print[Map[
      PieChart[#, SectorOrigin -> {Automatic, 1}, 
        LabelingFunction -> "RadialOutside", 
        ChartLegends -> {"0", "1", "2", "3", "4", "5", "6", "7", "8", 
          "9"}, ChartStyle -> "Pastel", 
        PlotLabel -> s /. {1 -> Text[Style["Pi", Large, Bold]], 
          2 -> Text[Style["E", Large, Bold]], 
          3 -> Text[Style["GoldenRatio", Large, Bold]], 
          4 -> Text[Style["Sqrt2", Large, Bold]]}] &, {c1, c2, c3, 
       c4}][[s]]], {s, 1, 4}]
  

Questions for the community:

• Question 1):

Does Mathematica already use the fastest method to calculate EulerGamma digits (I aborted after more than 5 hours)?

• Question 2):

Compiling NumericArray[] (compiled type) is set to new in V.12. Below is my attempt, did I do it right? How do I get the most out of this feature (my attempt got the same time and byte performance as NumericArray in the normal way)? How does it work?

cf = FunctionCompile[
  Function[Typed[arg, 
    TypeSpecifier["NumericArray"]["UnsignedInteger8", 1]], arg]]

EvaluationData[n = 1000000000;
 {z = cf[NumericArray[RealDigits[Pi, 10, n][[1]], 
     "UnsignedInteger8"]], ByteCount@z}]

Does anyone in the community know to answer any of the above questions to help me?

Thanks.