I try to solve the following expression:
Solve[100 - 20 x - 8 x^2 + x^3 == 0, {x}]
and get as output terms containing complicated expressions using the imaginary unit (highlight added by me).
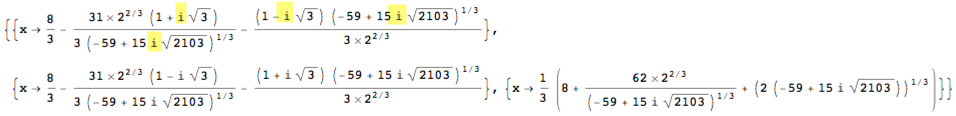
Evaluating the solutions numerically, it shows that they are all appearantly real:
N[Solve[100 - 20 x - 8 x^2 + x^3 == 0, {x}], 50]

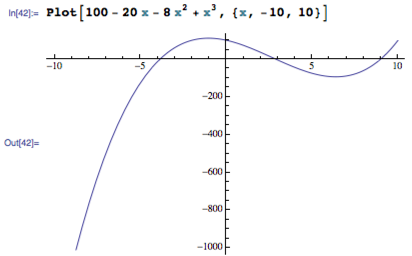
the imaginary part is 0. x 10^-50. A plot of the function also shows the real zeros at -3.8..., 2.8... and 8.9...:
Plot[100 - 20 x - 8 x^2 + x^3, {x, -10, 10}]
What can I do the have the result returned by Solve modified not to use complex numbers, but only square and cube roots?