Inspired by this, I did these two animations. Although there is already a built-in function KochCurve, but it can't do it directly and somewhat slow.

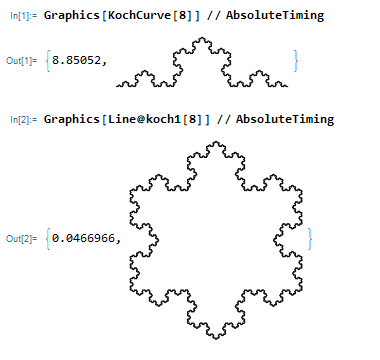
ClearAll[cf1];
cf1 = Compile[{{A, _Real, 2}, n}, 
   With[{d = RotateLeft[A] - A}, 
    Flatten[Transpose[
    {A, A + d/3, A + d.{{1/2, -n/(2 Sqrt[3])}, 
    {n/(2 Sqrt[3]), 1/2}}, A + (2 d)/3}], 1]
    ]
];

koch1[n_] := cf1[Nest[cf1[#, 1] &, CirclePoints[3], Floor[n]], FractionalPart[n]];

Manipulate[Graphics[{EdgeForm[Darker@Cyan], LightCyan, Polygon[koch1[n]]}, 
  PlotRange -> 1, ImageSize -> Large], {n, 0, 5}]


ClearAll[cf2];
cf2 = Compile[{{A, _Real, 2}, n}, 
   With[{d = RotateLeft[A] - A, ? = (n Pi)/3}, 
    Flatten[Transpose[
    {A, A + d/3, A + d.{{(1 + Cos[?])/3 , -Sin[?]/3}, {Sin[?]/3, (1 + Cos[?])/3}}, 
       A + d.{{1/2, -(1/6) Tan[?]}, {1/6 Tan[?], 1/2}}, 
       A + d.{{(2 - Cos[?])/3 , -Sin[?]/3}, {Sin[?]/3, (2 - Cos[?])/3}},
       A + (2 d)/3}], 1]
    ]
];

koch2[n_] := cf2[Nest[cf2[#, 1] &, CirclePoints[3], Floor[n]], FractionalPart[n]];

Manipulate[Graphics[{EdgeForm[Darker@Cyan], LightCyan, Polygon[koch2[n]]}, 
  PlotRange -> 1, ImageSize -> Large], {n, 0, 5}]

Attachments:

Koch snowflake i...nb