Please take a quick look at the documentation for Convolve:
reference.wolfram.com/mathematica/ref/Convolve.htmlConvolve requires 4 arguments. Additionally the examples show that it is meant to take symbolic functions, not numerical functions.
I don't want to complicate the math of this at all. But I should warn against using too many tools like interpolations if they are not needed. If you can resample the data set to keep it discrete and do a discrete convolution, I would recommend it instead of continuing down the path below.
Here's the definition of a convolution. I will use this with a couple of example InterpolationFunction expressions I've constructed.
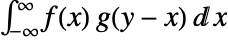
f = Interpolation[Table[{x, Sin[x]}, {x, 0, 10, 0.1}]];
g = Interpolation[Table[{x, Cos[E^x]}, {x, 0, 10, 0.1}]];
"f" and "g" are only defined from x = 0 to 10, so this will change the range of the integration. In short the integral is (I'm mostly sure):
Integrate[f[x]*g[y - x], {x, y, - y + 10}]
"y" of course must be between 0 and 10 for this to make sense.
Because f and g are not symbolic, they are numeric, we will have to use NIntegrate:
myConv[y_?NumericQ] := NIntegrate[f[x]*g[y - x], {x, y, y - 10}]
See
this article for why the function was defined with ?NumericQ.