First, some results, ParametricIPOPTMinimize code is attached as a separate notebook 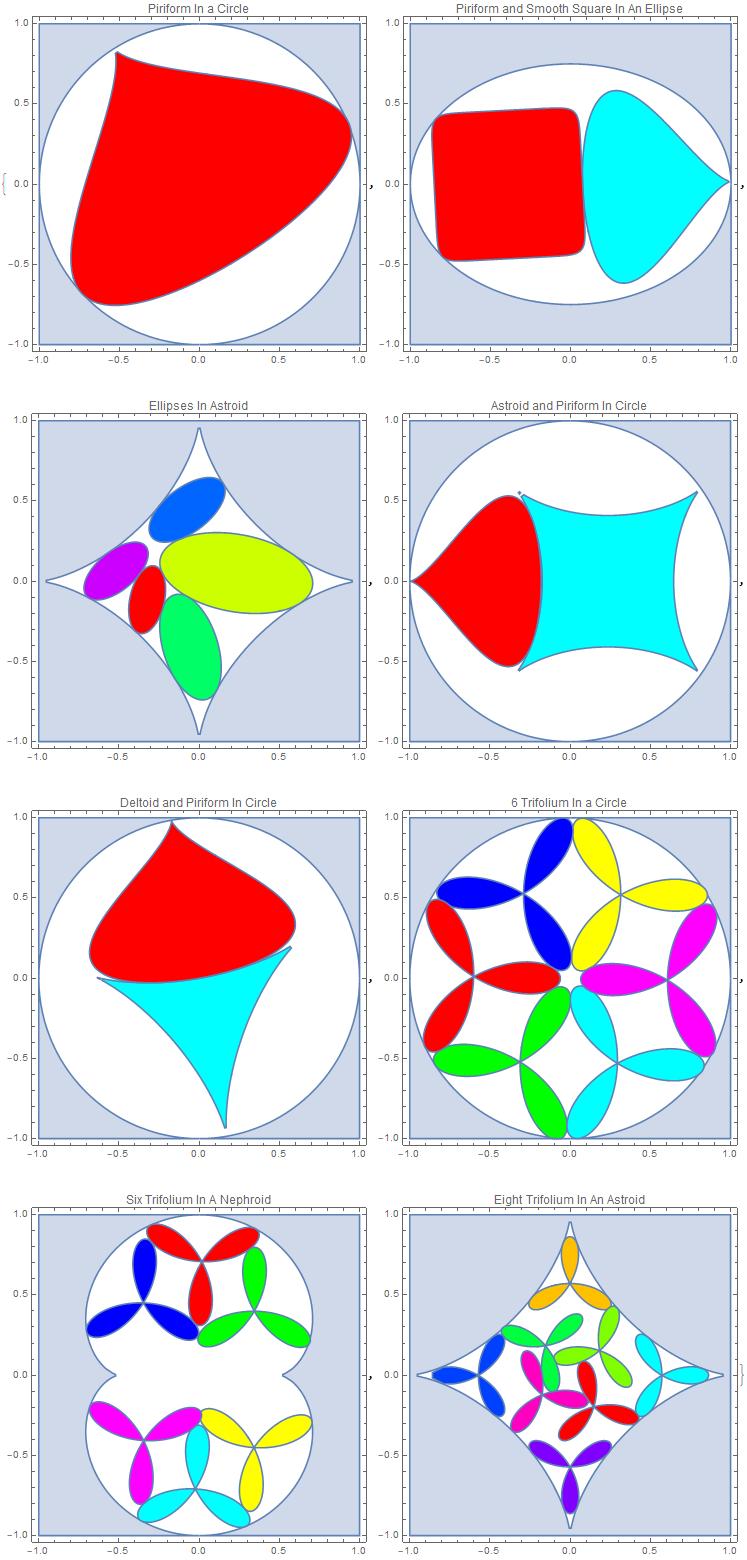
Set Up
(* rule to rotate and translate a curve given as a function of x and y *)
rottransrl[{xc_, yc_, \[Theta]_}, {x_, y_}] =
Thread[{x, y} -> RotationMatrix[-\[Theta]].{x - xc, y - yc}];
(* rule to rotate and translate a curve in which x and y are functions of a \
polar angle parameter p*)
rottransp[{xc_, yc_, \[Theta]_}][{cx_,
cy_}] = (RotationMatrix[\[Theta]].{cx, cy}) + {xc, yc};
(* curves given both as functions of x and y and as {x,y} coordinates \
parameterized by p *)
astroid[a_][xc_, yc_, \[Theta]_][x_,
y_] = (x^2 + y^2 - a^2)^3 + 27 a^2 x^2 y^2 /.
rottransrl[{xc, yc, \[Theta]}, {x, y}];
astroid[a_][xc_, yc_, \[Theta]_][p_] =
rottransp[{xc, yc, \[Theta]}][a {Cos[p]^3, Sin[p]^3}];
deltoid[a_][xc_, yc_, \[Theta]_][x_,
y_] = (x^2 + y^2)^2 - 8 a x (x^2 - 3 y^2) + 18 a^2 (x^2 + y^2) - 27 a^4 /.
rottransrl[{xc, yc, \[Theta]}, {x, y}];
deltoid[a_][xc_, yc_, \[Theta]_][p_] =
rottransp[{xc, yc, \[Theta]}][a {2 Cos[p] + Cos[2 p], 2 Sin[p] - Sin[2 p]}];
ell[n_, a_, b_][xc_, yc_, \[Theta]_][x_, y_] = (x/a)^n + (y/b)^n - 1 /.
rottransrl[{xc, yc, \[Theta]}, {x, y}];
ell[n_, a_, b_][xc_, yc_, \[Theta]_][p_] =
rottransp[{xc, yc, \[Theta]}][{a Sign[Cos[p]] Abs[Cos[p]]^(2/n),
b Sign[Sin[p]] Abs[Sin[p]]^(2/n)}];
neph[a_][xc_, yc_, \[Theta]_][x_, y_] = (x^2 + y^2 - 4 a^2)^3 - 108 a^4 y^2 /.
rottransrl[{xc, yc, \[Theta]}, {x, y}];
neph[a_][xc_, yc_, \[Theta]_][p_] =
rottransp[{xc, yc, \[Theta]}][a {3 Cos[p] - Cos[3 p], 3 Sin[p] - Sin[3 p]}];
piri[a_, b_][xc_, yc_, \[Theta]_][x_, y_] =
a^4 y^2 - b^2 x^3 (2 a - x) /. rottransrl[{xc, yc, \[Theta]}, {x, y}];
piri[a_, b_][xc_, yc_, \[Theta]_][p_] =
rottransp[{xc, yc, \[Theta]}][ {a (1 + Sin[p]), b Cos[p] (1 + Sin[p])}];
trifol[a_][xc_, yc_, \[Theta]_][x_,
y_] = (x^2 + y^2) (y^2 + x (x + a)) - 4 a x y^2 /.
rottransrl[{xc, yc, \[Theta]}, {x, y}];
trifol[a_][xc_, yc_, \[Theta]_][p_] =
rottransp[{xc, yc, \[Theta]}][- a Cos[3 p] {Cos[p], Sin[p]}];
(* evaluate function describing curve 1 at point parameterized by p on curve \
2 *)
fcc[curve1_, curve2_] := curve1[x, y] /. Thread[{x, y} -> curve2[p]]
(* set up packing problem with outer curve, inner curves, optimization \
objective, extra constraints and variables with bounds and number of \
parametric points used *)
packSetUp[rawOuterCurve_, rawInnerCurves_List, objective_, extracons_List,
extraVWB_List, regbnd_, nPoints_Integer] :=
Block[{nCurves = Length[rawInnerCurves], p , iter, outerCurve, innerCurves,
xc, yc, \[Theta], cin1, cin2, cin3, cno1, cno2, cno3, allcons, vwb},
(* make center of outer curve {0,0} with orientation \[Theta] = 0 *)
outerCurve = rawOuterCurve[0, 0, 0];
(* add center and orientation variables to inner curves *)
innerCurves =
Table[rawInnerCurves[[i]][xc[i], yc[i], \[Theta][i]], {i, nCurves}];
(* points on inner curves are inside outer curve *)
cin1 = Table[
fcc[outerCurve, innerCurves[[i]]] <= 0, {i, nCurves}, {p, 2 \[Pi]/nPoints,
2 \[Pi], 2 \[Pi]/nPoints}];
(* points on outer curve are outside inner curves *)
cin2 = Table[
fcc[innerCurves[[i]], outerCurve] >= 0, {i, nCurves}, {p, 2 \[Pi]/nPoints,
2 \[Pi], 2 \[Pi]/nPoints}];
(* centers of inner curves are inside outer curves *)
cin3 = Table[outerCurve[xc[i], yc[i]] <= 0, {i, nCurves}];
(* points inner curves are outside other inner curves *)
cno1 = Table[
fcc[innerCurves[[i]], innerCurves[[j]]] >= 0, {i, nCurves - 1}, {j, i + 1,
nCurves}, {p, 2 \[Pi]/nPoints, 2 \[Pi], 2 \[Pi]/nPoints}];
cno2 = Table[
fcc[innerCurves[[j]], innerCurves[[i]]] >= 0, {i, nCurves - 1}, {j, i + 1,
nCurves}, {p, 2 \[Pi]/nPoints, 2 \[Pi], 2 \[Pi]/nPoints}];
(* center of inner curves are outside other inner curves *)
cno3 = Table[
innerCurves[[i]][xc[j], yc[j]] >= 0.001, {i, nCurves - 1}, {j, i + 1,
nCurves}];
(* combine constraints *)
allcons = Flatten[{cin1, cin2, cin3, cno1, cno2, cno3, extracons}];
(* put bounds on variables for ipopt *)
vwb = Join[
Flatten[Table[{{xc[i], -regbnd, regbnd}, {yc[i], -regbnd,
regbnd}, {\[Theta][i], 0, 2 \[Pi]}}, {i, nCurves}], 1], extraVWB];
{objective, allcons, vwb}
]
(* plot solution given outer curve, inner curves, optimization solution and \
plotting bounds *)
plt[rawOuterCurve_, rawInnerCurves_List, sln_, bnd_, label_] :=
Block[{nCurves = Length[rawInnerCurves], innerCurvesxy},
innerCurvesxy =
Table[rawInnerCurves[[i]][xc[i], yc[i], \[Theta][i]][x, y], {i, nCurves}] /.
sln[[2]];
Show[
RegionPlot[
rawOuterCurve[0, 0, 0][x, y] >= 0, {x, -bnd, bnd}, {y, -bnd, bnd}],
Table[RegionPlot[innerCurvesxy[[i]] <= 0, {x, -bnd, bnd}, {y, -bnd, bnd},
PlotStyle -> Hue[i/nCurves], MaxRecursion -> 5], {i, nCurves}],
PlotLabel -> label, ImageSize -> Medium]
]
(* perform packing usng randomly chosen starting values for variables and \
plot result *)
packPlot[rawOuterCurve_, rawInnerCurves_List, objective_, extracons_List,
extraVWB_List, regbnd_, nPoints_Integer, {nRands_Integer, seed_Integer},
label_] :=
Block[{pack =
packSetUp[rawOuterCurve, rawInnerCurves, objective, extracons, extraVWB,
regbnd, nPoints], res},
res = iMin[Sequence @@ pack, {nRands, seed}];
Print[res];
plt[ rawOuterCurve, rawInnerCurves, res, regbnd, label]
]
Pack
Piriform Curve In a Circle
plt[1] = packPlot[ell[2, 1, 1], {piri[a, a]}, -a, {}, {{a, 0, 1}}, 1,
25, {5, 0}, "Piriform In a Circle"];
{{Solve_Succeeded,5}}
{-0.762352,{xc[1]->-0.53459,yc[1]->0.845111,\[Theta][1]->5.27808,a->0.762352},Solve_Succeeded}
Piriform Curve and a Smooth Square In an Ellipse
plt[2] = packPlot[
ell[2, 1, 3/4], {piri[a, a], ell[10, a, a]}, -a, {}, {{a, 0, 1}}, 1,
25, {10, 0}, "Piriform and Smooth Square In An Ellipse"];
{{Solve_Succeeded,8},{Maximum_Iterations_Exceeded,1},{Infeasible_Problem_Detected,1}}
{-0.462603,{xc[1]->0.999731,yc[1]->0.0174043,\[Theta][1]->3.19062,xc[2]->-0.388133,yc[2]->-0.00172318,\[Theta][2]->0.0512254,a->0.462603},Solve_Succeeded}
5 Unequal Ellipses In an Astroid Curve
plt[3] = packPlot[astroid[1],
Table[ell[2, r*i^(-1/2), r*i^(-1/2)/2], {i, 5}], -r, {}, {{r, 0, 1}}, 1,
25, {20, 0}, "Ellipses In Astroid"];
{{Solve_Succeeded,7},{Infeasible_Problem_Detected,7},{Maximum_Iterations_Exceeded,5},{Restoration_Failed,1}}
{-0.482296,{xc[1]->0.23132,yc[1]->0.0508214,\[Theta][1]->6.10473,xc[2]->-0.0540852,yc[2]->-0.41056,\[Theta][2]->1.87279,xc[3]->-0.0751668,yc[3]->0.445078,\[Theta][3]->0.649836,xc[4]->-0.518079,yc[4]->0.0636028,\[Theta][4]->0.697771,xc[5]->-0.324416,yc[5]->-0.115101,\[Theta][5]->4.4973,r->0.482296},Solve_Succeeded}
Astroid and Piriform Curve In a Circle
plt[4] = packPlot[
ell[2, 1, 1], {astroid[r],
piri[r/2, r/2]}, -r, {\[Theta][2] == 0}, {{r, .5, 1.5}}, 1, 20, {20, 0},
"Astroid and Piriform In Circle"];
{{Solve_Succeeded,8},{Infeasible_Problem_Detected,12}}
{-0.819537,{xc[1]->0.235472,yc[1]->-8.09483*10^-9,\[Theta][1]->2.35619,xc[2]->-1.,yc[2]->4.36511*10^-8,\[Theta][2]->6.30584*10^-44,r->0.819537},Solve_Succeeded}
Deltoid and Piriform In a Circle
plt[5] = packPlot[
ell[2, 1, 1], {deltoid[r], piri[2 r, 2 r]}, -r, {}, {{r, 0, 1}}, 1,
20, {20, 0}, "Deltoid and Piriform In Circle"];
{{Solve_Succeeded,17},{Infeasible_Problem_Detected,3}}
{-0.25,{xc[1]->0.0447201,yc[1]->-0.245972,\[Theta][1]->4.88445,xc[2]->-0.173134,yc[2]->0.984898,\[Theta][2]->4.88837,r->0.25},Solve_Succeeded}
6 Trifolium Curves in a Circle
plt[6] = packPlot[ell[2, 1, 1], Table[trifol[a], 6], -a, {}, {{a, 0, 1}}, 1,
25, {5, 0}, "6 Trifolium In a Circle"];
{{Solve_Succeeded,5}}
{-0.540812,{xc[1]->0.3152,yc[1]->0.520018,\[Theta][1]->3.13499,xc[2]->-0.311793,yc[2]->-0.522068,\[Theta][2]->2.0649,xc[3]->0.294457,yc[3]->-0.530461,\[Theta][3]->3.11475,xc[4]->-0.290702,yc[4]->0.526852,\[Theta][4]->2.08244,xc[5]->0.606595,yc[5]->-0.0116766,\[Theta][5]->2.08514,xc[6]->-0.601647,yc[6]->0.0100492,\[Theta][6]->3.11745,a->0.540812},Solve_Succeeded}
6 Trifolium Curves in a Nephroid
plt[7] = packPlot[neph[1/4], Table[trifol[a], 6], -a, {}, {{a, 0, 1}}, 1,
25, {5, 0}, "Six Trifolium In A Nephroid"];
{{Solve_Succeeded,5}}
{-0.39834,{xc[1]->0.341793,yc[1]->-0.451307,\[Theta][1]->5.69289,xc[2]->0.343549,yc[2]->0.39922,\[Theta][2]->4.70635,xc[3]->-0.0242371,yc[3]->-0.708855,\[Theta][3]->4.6588,xc[4]->-0.347635,yc[4]->0.450998,\[Theta][4]->0.492849,xc[5]->-0.345656,yc[5]->-0.407266,\[Theta][5]->3.60394,xc[6]->0.0174008,yc[6]->0.708026,\[Theta][6]->1.53523,a->0.39834},Solve_Succeeded}
8 Trifolium Curves In an Astroid
plt[8] = packPlot[astroid[1], Table[trifol[a], 8], -a, {}, {{a, 0, 1}}, 1,
25, {5, 0}, "Eight Trifolium In An Astroid"];
{{Solve_Succeeded,5}}
{-0.291771,{xc[1]->-0.00118292,yc[1]->0.57197,\[Theta][1]->0.523553,xc[2]->0.183403,yc[2]->0.153518,\[Theta][2]->2.28228,xc[3]->-0.153617,yc[3]->0.183786,\[Theta][3]->5.93085,xc[4]->0.571947,yc[4]->-0.000825772,\[Theta][4]->1.04846,xc[5]->-0.571964,yc[5]->-0.00109543,\[Theta][5]->2.09405,xc[6]->0.0000907175,yc[6]->-0.571793,\[Theta][6]->1.57035,xc[7]->-0.174907,yc[7]->-0.121972,\[Theta][7]->0.892891,xc[8]->0.147927,yc[8]->-0.196277,\[Theta][8]->4.95108,a->0.291771},Solve_Succeeded}
Table[plt[i], {i, 8}]
 Attachments:
Attachments: