Hello and happy New year to the Wolfram Team.
I recently tried to compute a Sum, used to derive an adsorbtion isotherm (see reference at the end). The basic equation is a sum of binomials:
Z[N]=Binomial[L/m,Nt]*Product[Binomial[m,n],{n,1,Nt}]*q^Nt
S[N, mu]=Sum[Z[Nt]*a^Nt, {Nt,0,L}]
The result is terrible, with lenghty and complicated functions. Somehow the authors of the paper replaced the parameter Nt with a new variable, called "s" and defined as:
s=Sum[n,{n,1,Nt}]/Nt
And ended up with this:
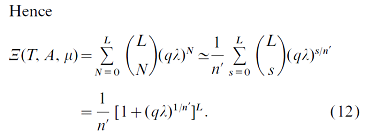
The problem is that as Nt is replaced with a function, the program doesn't recognize the parameter Nt= s/n as an iterator, and sends an error message. In the Wolfram documentation is suggested (see attached printscreen) that there is a way to resolve this obstacle, but I could not find a relevant example.
Thank you in advance for your help,
Regards,
Alberto
REFERENCE:
F. Kano et al. / Surface Science 467 (2000) 131138
"Fractal model for adsorption on activated carbon surfaces: Langmuir and Freundlich adsorption"
 Attachments:
Attachments: