Introduction:

Dattatreya Ramchandra Kaprekar (1905–1986) created a mathematical routine, the Kaprekar´s routine, which is an iterative algorithm that takes a natural number and creates two new numbers, sorting the digits of the initial number in descending and ascending order, and then subtracts the second of the first to provide the natural number for the next iteration. Consequently, he found that 3-digit numbers always arrive at a constant (Kaprekar constant) equal to 495 and 4-digit numbers always converge at a constant (Kaprekar constant) equal to 6174. Another number of digits can only generate cycles or cycles with also other Kaprekar´s constant in a given smaller proportion.

Objective:

The goal is to test the results of Kaprekar´s routines using numbers with 5, 6, 7 and 8 digits, creating a graphic impression of the cycles. The results should provide information such as: number of iterations until the cycles are found, number of terms in the cycles, if any number converges to a Kaprekar´s constant for a number of digits greater than 4, specific graphic impressions of the cycles for a specific number of digits and the proportions of each result.

Test of the Method (with 3 and 4 digit numbers):

In this work, I used all the numbers with a certain number of digits sequentially as a sample, covering all the numbers (with 3, 4, 5, 6 and 7 digits). The exception is the final impression with all the 8 digit numbers that I had to use a random distributed sample to run the test as explained later.

In some results of the Kaprekar´s routine, the numbers converge to 0, in cases such as: equal digits (1111), other numbers (2111), etc. In all tests in this work, I excluded the results that converge to 0, as for example, if I used 9000 numbers in the sample (4 digits), the result may have used only 8923 (that is, the difference is the excluded ones that converge to 0).

To test the code, I intended to arrive at the same result for the Kaprekar´s constants, with 3 digits being 495 and 4 digits being 6174.

For example, below, a code to generate random numbers and a code to make the successive iterations of the routine until reaching the converence:

d = 4;
b = 10;
z = RandomInteger[{FromDigits@PadRight[{1}, d], 
   FromDigits@Table[9, d]}]

Do[Do[z = 
   FromDigits@Sort[IntegerDigits[z, b], Greater] - 
    FromDigits@Sort@IntegerDigits[z, b], 1]; Print[z], 10]

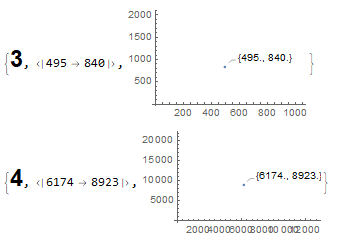
Confirming the Kaprekar constants for all numbers with 3 and 4 digits (all 900 and 9000 numbers respectively):

d = {3, 4};
b = 10;
n = {900, 9000};
k = DeleteCases[
   Table[z = 
     Range[FromDigits@PadRight[{1}, d[[1]]], 
       FromDigits@Table[9, d[[1]]]][[ss1]];
    Do[z = 
      FromDigits@Sort[IntegerDigits[z, b], Greater] - 
       FromDigits@Sort@IntegerDigits[z, b], 15]; z, {ss1, 1, n[[1]]}],
    0];
kb = DeleteCases[
   Table[zb = 
     Range[FromDigits@PadRight[{1}, d[[2]]], 
       FromDigits@Table[9, d[[2]]]][[ss2]];
    Do[zb = 
      FromDigits@Sort[IntegerDigits[zb, b], Greater] - 
       FromDigits@Sort@IntegerDigits[zb, b], 15]; 
    zb, {ss2, 1, n[[2]]}], 0];
Do[Print[{{Text[Style[d[[1]], Bold, Large]], Counts@Sort@k, 
     ListLinePlot[Tooltip@SortBy[Tally@k, First], 
      LabelingFunction -> (Callout[#1, Automatic] &), 
      PlotRange -> All, ImageSize -> Small]}, {Text[
      Style[d[[2]], Bold, Large]], Counts@Sort@kb, 
     ListLinePlot[Tooltip@SortBy[Tally@kb, First], 
      LabelingFunction -> (Callout[#1, Automatic] &), 
      PlotRange -> All, ImageSize -> Small]}}[[fs]]], {fs, 1, 2}]

Thus, samples were generated to be able to calculate all numbers with specific numbers of digits. In the example below, it was done with 3 and 4 digits simultaneously:

d1 = {3, 4}; b1 = 10; it1 = 15; it2 = 20;
z1 = {Range[FromDigits@PadRight[{1}, d1[[1]]], 
    FromDigits@Table[9, d1[[1]]]], 
   Range[FromDigits@PadRight[{1}, d1[[2]]], 
    FromDigits@Table[9, d1[[2]]]]};

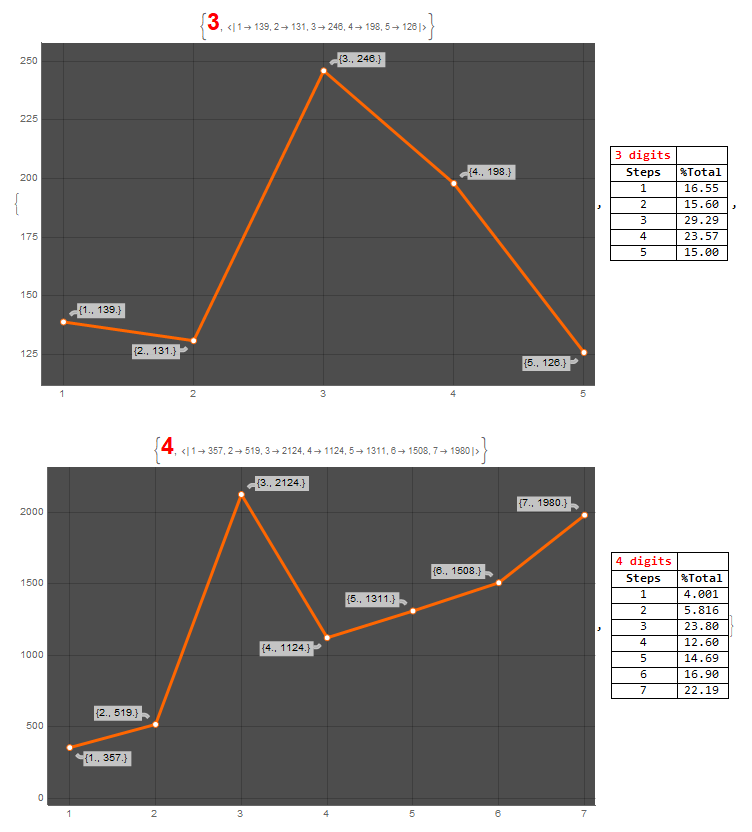
Using the following code, we obtained the number of iterations necessary to reach the Kaprekar´s constants with 3 and 4 digits:

u1 = Sort@
  Normal@Counts@
    Table[z2 = z1[[1, t]]; 
     e1 = Tally@
       Table[Do[
         z2 = FromDigits@Sort[IntegerDigits[z2, b1], Greater] - 
           FromDigits@Sort@IntegerDigits[z2, b1], 1]; z2, it1]; 
     e10 = DeleteCases[
       If[MemberQ[
          Table[If[
            ContainsOnly[
              IntegerDigits[
               e1[[x, 1]]], {IntegerDigits[e1[[x, 1]]][[1]]}] == 
             True, {}, e1[[x]]], {x, 1, Length@e1}], {}] == True, {}, 
        e1], {}]; e2 = CountsBy[e10, Last]; 
     e3 = If[e2 == <||>, 0, 
       If[MemberQ[Keys@e2, 1] == False, 1, (1 /. e2) + 1]]; 
     e3, {t, 1, Length@(z1[[1]])}]; u1b = 
 Sort@Normal@Counts@Table[z2b = z1[[2, t]];
     e1b = 
      Tally@Table[
        Do[z2b = 
          FromDigits@Sort[IntegerDigits[z2b, b1], Greater] - 
           FromDigits@Sort@IntegerDigits[z2b, b1], 1]; z2b, it2]; 
     e10b = DeleteCases[
       If[MemberQ[
          Table[If[
            ContainsOnly[
              IntegerDigits[
               e1b[[x, 1]]], {IntegerDigits[e1b[[x, 1]]][[1]]}] == 
             True, {}, e1b[[x]]], {x, 1, Length@e1b}], {}] == 
         True, {}, e1b], {}];
     e2b = CountsBy[e10b, Last]; 
     e3b = 
      If[e2b == <||>, 0, 
       If[MemberQ[Keys@e2b, 1] == False, 1, (1 /. e2b) + 1]]; 
     e3b, {t, 1, Length@(z1[[2]])}]; v1 = 
 AssociationThread[
  DeleteCases[Keys[u1], 0] -> (DeleteCases[Keys[u1], 0] /. u1)]; v1b =
  AssociationThread[
  DeleteCases[Keys[u1b], 0] -> (DeleteCases[Keys[u1b], 0] /. u1b)];

Do[Print[{ListLinePlot[Tooltip@v1, 
    LabelingFunction -> (Callout[#1, Automatic, Scaled[1.5]] &), 
    PlotLabel -> {Text[Style[d1[[1]], Large, Bold, Red]], 
      Text[Style[v1, Small]]}, PlotTheme -> "Marketing", 
    PlotRange -> All, ImageSize -> Large], 
   Grid[Join[{{Style["3 digits", Red, Bold]}, {Style["Steps", Bold], 
       Style["%Total", Bold]}}, 
     Thread[{Range@5, 
       N[100*(Range@5 /. v1)/Total@(Range@5 /. v1), 4]}]], 
    Frame -> All], 
   ListLinePlot[Tooltip@v1b, 
    LabelingFunction -> (Callout[#1, Automatic, Scaled[1.5]] &), 
    PlotLabel -> {Text[Style[d1[[2]], Large, Bold, Red]], 
      Text[Style[v1b, Small]]}, PlotTheme -> "Marketing", 
    PlotRange -> All, ImageSize -> Large], 
   Grid[Join[{{Style["4 digits", Red, Bold]}, {Style["Steps", Bold], 
       Style["%Total", Bold]}}, 
     Thread[{Range@7, 
       N[100*(Range@7 /. v1b)/Total@(Range@7 /. v1b), 4]}]], 
    Frame -> All]}], 1]

• Test result of the method:

The Kaprekar constants for 3 and 4 digits were confirmed and, for 3 digits, the maximum number of iterations to converge is 5, while for 4 digits the maximum number of iterations to converge is 7. All proportions were shown in the result.

Analysis for 5 and 6 digits:

Natural numbers with the number of digits equal to 5 and 6 form cycles as a result of the Kaprekar´s routine. Below is an example of a 5 digit random number showing its cycle (in this case, it took 5 iterations to start the cycle and the cycle has 4 terms):

Do[Do[z = 
   FromDigits@Sort[IntegerDigits[z, b], Greater] - 
    FromDigits@Sort@IntegerDigits[z, b], 1]; Print[z], 15]

Generating lists of all natural numbers with 5 and 6 digits (all 90000 and 900000 respectively), we find the result for the number of necessary iterations until the cycles start:

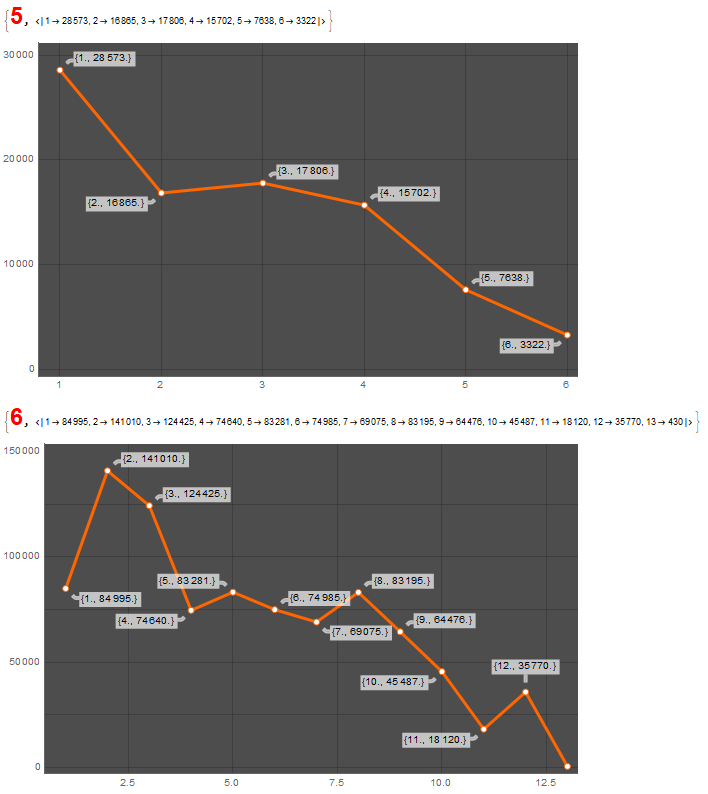
The maximum number of iterations to start a cycle with the 5-digit numbers is 6 and the maximum number of iterations to start a cycle with the 6-digit numbers is 13.

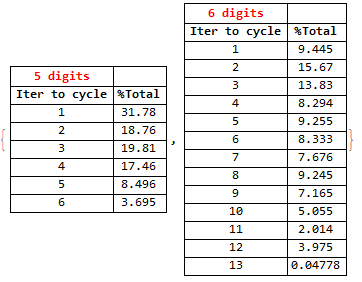
The result, as a percentage, of the number of iterations for all 5 and 6 digit numbers:

Using the following code, we have the number (and percentage) of terms that make up a cycle for all 5-digit numbers:

d1 = 5; b1 = 10; z1 = 
 Range[FromDigits@PadRight[{1}, d1], FromDigits@Table[9, d1]];
u1 = Table[it = 20; z2 = z1[[t]];
   e1 = Tally@
     Table[Do[
       z2 = FromDigits@Sort[IntegerDigits[z2, b1], Greater] - 
         FromDigits@Sort@IntegerDigits[z2, b1], 1]; z2, it];
   e10 = DeleteCases[
     If[MemberQ[
        Table[If[
          ContainsOnly[
            IntegerDigits[
             e1[[x, 1]]], {IntegerDigits[e1[[x, 1]]][[1]]}] == 
           True, {}, e1[[x]]], {x, 1, Length@e1}], {}] == True, {}, 
      e1], {}];
   Length@DeleteCases[e10, {_, 1}], {t, 1, Length@z1}];
x1 = Counts@Table[u1[[f]], {f, 1, Length@u1}]; kk1 = 
 AssociationThread[
  DeleteCases[Keys[x1], 0] -> (DeleteCases[Keys[x1], 0] /. x1)];

Grid[Join[{{Style["5 digits", Bold, Red]}, {Style["Steps in Cycle", 
     Bold], Style["Value", Bold], Style["%Total", Bold]}}, 
  Thread[{Keys@kk1, (Keys@kk1 /. kk1), 
    N[100*(Keys@kk1 /. kk1)/Total[Keys@kk1 /. kk1], 4]}]], 
 Frame -> All]

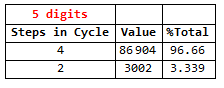
For d1 = 6 (6-digit numbers), we have the number of terms in a cycle for 6-digit numbers. Where there is 1 term per cycle, it is where it converged in constants and this occurred in some of these numbers, that is, some numbers converged. The proportion of these numbers is also shown:

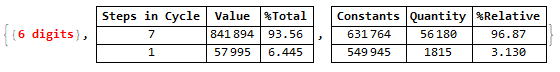
Finally, to create the impression for 5 digits, I defined some iteration intervals (sections), multiples of 4 and 2, because they are the number of terms in 5-digit cycles (in this case, I used sections with 4 different iteration numbers: {20,21,22,23}) and each with all 90000 numbers with 5 digits.

d = 5; b = 10; n = 90000;
Do[k = DeleteCases[
   Table[z = 
     Range[FromDigits@PadRight[{1}, d], FromDigits@Table[9, d]][[ss]];
    Do[z = 
      FromDigits@Sort[IntegerDigits[z, b], Greater] - 
       FromDigits@Sort@IntegerDigits[z, b], f]; z, {ss, 1, n}], 0];
 Print[{Text[Style[d, Bold, Large]], Text[Style[f, Bold, Red]], 
   SortBy[Tally@k, First]}], {f, {20, 21, 22, 23}}]

Combining the values, we can cover the entire result for all the numbers in each term position in a cycle, finally showing the impression of the cycles generated from the 5-digit number.

r1 = {{53955, 844}, {59994, 2158}, {61974, 12680}, {62964, 
    11514}, {63954, 10946}, {71973, 5852}, {74943, 18194}, {75933, 
    10368}, {82962, 9776}, {83952, 7574}};
r2 = {{53955, 2158}, {59994, 844}, {61974, 10946}, {62964, 
    18194}, {63954, 10368}, {71973, 11514}, {74943, 7574}, {75933, 
    9776}, {82962, 12680}, {83952, 5852}};
r3 = {{53955, 844}, {59994, 2158}, {61974, 10368}, {62964, 
    7574}, {63954, 9776}, {71973, 18194}, {74943, 5852}, {75933, 
    12680}, {82962, 10946}, {83952, 11514}};
r4 = {{53955, 2158}, {59994, 844}, {61974, 9776}, {62964, 
    5852}, {63954, 12680}, {71973, 7574}, {74943, 11514}, {75933, 
    10946}, {82962, 10368}, {83952, 18194}};

vv = GatherBy[Flatten[{r1, r2, r3, r4}, 1], First];
uu = Table[{vv[[j]][[1, 1]], 
    Sum[vv[[j]][[i, 2]], {i, 1, Length@(vv[[j]])}]}, {j, 1, 
    Length@vv}];
ww = Table[uu[[g, 1]] -> uu[[g, 2]], {g, 1, Length@uu}];
Grid[Join[{{Style["5 digits", Bold, Red]}, {Style["Number", Bold], 
    Style["Quantity", Bold], Style["%Total", Bold]}}, 
  Thread[{Keys@ww, (Keys@ww /. ww), 
    N[100*(Keys@ww /. ww)/Total[Keys@ww /. ww], 4]}]], Frame -> All]
ListLinePlot[Style[Tooltip@uu, Purple], 
 LabelingFunction -> (Callout[#1, Automatic, Scaled[1.5]] &), 
 Mesh -> Full, Filling -> Automatic, AxesStyle -> Directive[Red, 12], 
 PlotRange -> All, ImageSize -> Large]

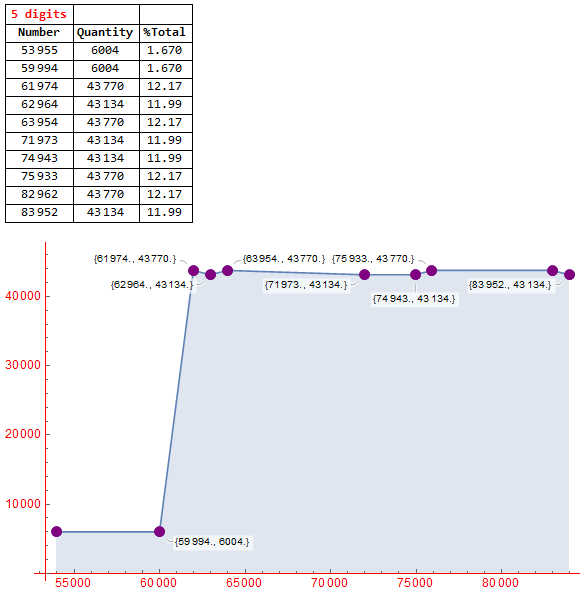
If we choose a random number with 5 digits and iterate until we form cycles, the chance of the result being in this proportion above is extremely high.

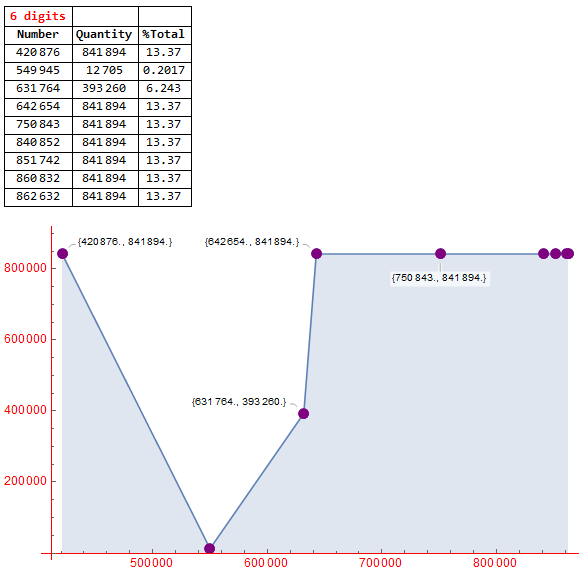
Likewise, to have the impression of cycles for numbers with 6 digits (d = 6, n = 900000, f(iter) = {30,31,32,33,34,35,36}), a number of sections multiple of 7 and 1 was generated for the iterations (I used 7 and each with all 900000 6-digit numbers, to cover all possible terms within a cycle). After using a code similar to the 5-digit code, the result below was generated for 6 digits and shows the impression of the cycles for that specific number of digits:

7-digit analysis:

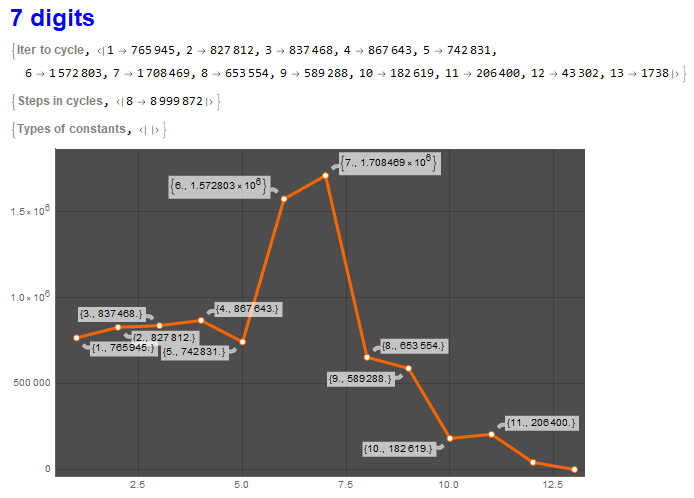
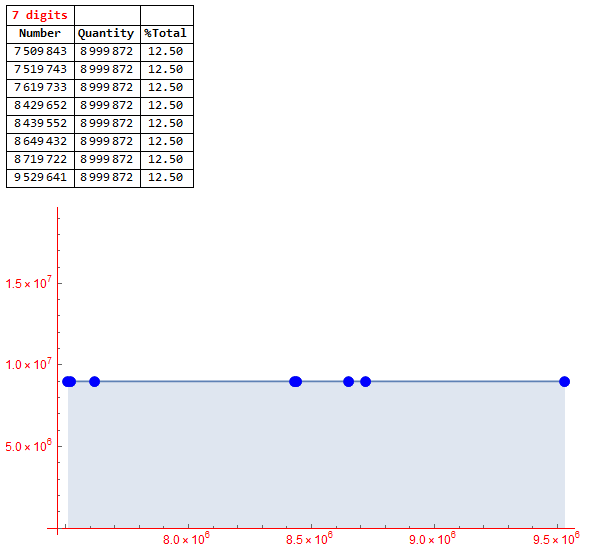
Below, we can see that, for numbers with 7 digits, the maximum number of iterations to form cycles using the Kaprekar´s routine is 13 steps (iterations) and the number of terms in the 7-digit cycle is always 8. The list of numbers was generated with the code similar to the ones already used.

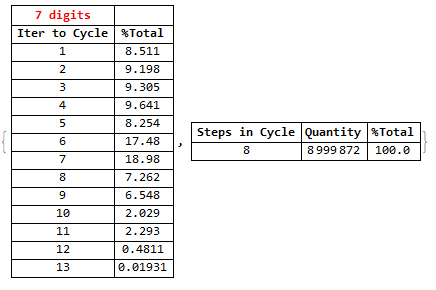
• Result (as a percentage) for all 7-digit numbers (note that there is no convergence to any Kaprekar constant using all 7-digit numbers):

To generate the impression of cycles coming from numbers with 7 digits, I used a number of sections multiple of 8 (I used 8), because it is the number of terms in a cycle formed by this number of digits. Below is the impression (note that, for 7-digit numbers, the chance is perfectly equal to finding a term number for the cycle when executing the Kaprekar´s routine):

8 digits:

There are 90000000 numbers with 8 digits. For my machine to be able to perform a task with this quantity of numbers (each number has 35 iterations in the code), I divided this total quantity into the 7 parts below:

d1 = 8; b1 = 10;
z0 = NumericArray[Range[10000000, 39999999], "UnsignedInteger32"];
z1 = NumericArray[Range[40000000, 49999999], "UnsignedInteger32"];
z1b = NumericArray[Range[50000000, 59999999], "UnsignedInteger32"];
z1c = NumericArray[Range[60000000, 69999999], "UnsignedInteger32"];
z1d = NumericArray[Range[70000000, 79999999], "UnsignedInteger32"];
z1e = NumericArray[Range[80000000, 89999999], "UnsignedInteger32"];
z1f = NumericArray[Range[90000000, 99999999], "UnsignedInteger32"];

I was able to calculate all numbers (with 8 digits) and the result was added below to provide how many iterations to reach a cycle, the number of terms in each cycle and the Kaprekar constants with 8 digits, using a code similar to the one already used. That´s the result:

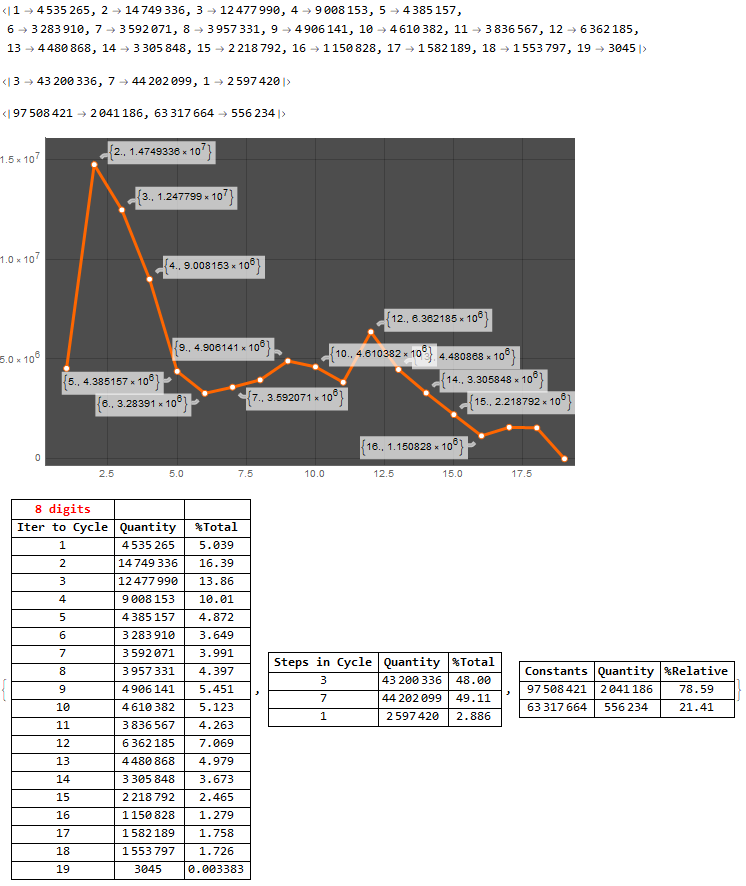
But, to have the impression of the cycle with numbers of 8 digits, it was not possible to do it in the same way as the previous ones, because it lacked computational power.

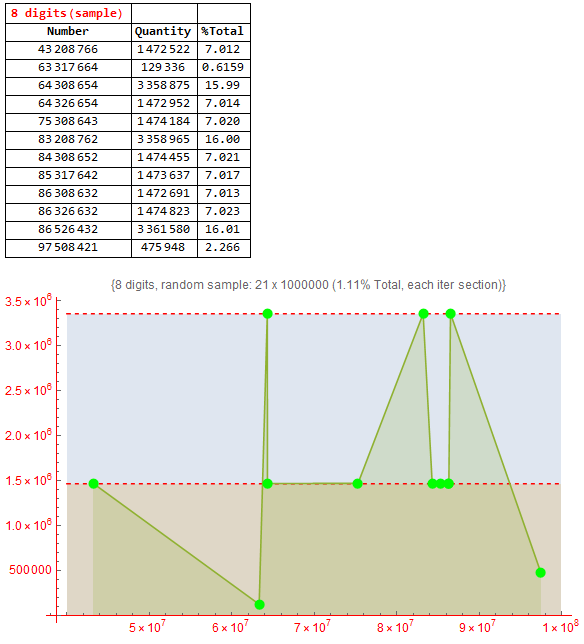
I had to do 21 sections with a certain number of iterations because the number of terms per cycle can be 3, 7 or 1, the smallest possible multiple of those numbers is 21. So, it would be 21 x 90000000. To get around this, I generated a sample well distributed using 21 x 1000000 random numbers with 8 digits as follows (f(iter) = {35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55}):

d = 8; b = 10;
Do[k = DeleteCases[
   Table[z = 
     RandomInteger[{FromDigits@PadRight[{1}, d], 
       FromDigits@Table[9, d]}];
    Do[z = 
      FromDigits@Sort[IntegerDigits[z, b], Greater] - 
       FromDigits@Sort@IntegerDigits[z, b], f]; z, 1000000], 0];
 Print[{Text[Style[d, Bold, Large]], Text[Style[f, Bold, Red]], 
   SortBy[Tally@k, First]}], {f, {35, 36, 37, 38, 39, 40, 41, 42, 43, 
   44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55}}]

Combining the result from the 21 sections of iteration, I could see an outline of what the cycle impression would look like with 8 digit numbers. The values in the result are not exact because I used only 1.11% of the 90000000 at random in each of the 21 sections. Just so we can get an idea of what that impression looks like:

vv = GatherBy[
   Flatten[{r35, r36, r37, r38, r39, r40, r41, r42, r43, r44, r45, 
     r46, r47, r48, r49, r50, r51, r52, r53, r54, r55}, 1], First];
uu = Table[{vv[[j]][[1, 1]], 
    Sum[vv[[j]][[i, 2]], {i, 1, Length@(vv[[j]])}]}, {j, 1, 
    Length@vv}];
ww = Table[uu[[g, 1]] -> uu[[g, 2]], {g, 1, Length@uu}];
Grid[Join[{{Style["8 digits(sample)", Bold, Red]}, {Style["Number", 
     Bold], Style["Quantity", Bold], Style["%Total", Bold]}}, 
  Thread[{Keys@ww, (Keys@ww /. ww), 
    N[100*(Keys@ww /. ww)/Total[Keys@ww /. ww], 4]}]], Frame -> All]
ListLinePlot[{Style[{{4.0*10^7, 3.36*10^6}, {10*10^7, 3.36*10^6}}, 
   Dashed, Red], 
  Style[{{4.0*10^7, 1.47*10^6}, {10*10^7, 1.47*10^6}}, Dashed, Red], 
  Style[Tooltip@uu, Green]}, Filling -> Automatic, 
 AxesStyle -> Directive[Red, 12], PlotRange -> All, 
 PlotLabel -> {"8 digits, random sample: 21 x 1000000 (1.11% Total, \
each iter section)"}, ImageSize -> Large]

Overall result:

The confirmation of the method of this work for the Kaprekar constants with 3 and 4 digits was true.

The 5, 6 and 7 digit study was a considered a success, as all numbers with this number of digits were used as sample, showing the probabilities after choosing a random number and after the Kaprekar´s routine arrives in a cycle.

It was confirmed that only a few 6-digit numbers generate two different Kaprekar constants and data on their proportions and chances were also found.

A satisfactory result was to have found two Kaprekar constants for some numbers with 8 digits, despite the great majority of the numbers having generated cycles. The proportions of iterations up to one cycle (max 19), the number of terms in one cycle and the proportions of the Kaprekar constant for 8 digits were successful, as all 90000000 numbers were used for these measurements. The graphic impression for the cycle for this number of digits was a partial success, as only a sample of numbers was used and not all as already discussed. Therefore, there are no precise values of their proportions in the final impression, just a graphic sketch of how it should be.

Perhaps one day with greater computational power, improved code, etc., I will be able to do this work with a greater number of digits (9, 10, etc.) and with greater precision in a large number of digits.

Thanks.