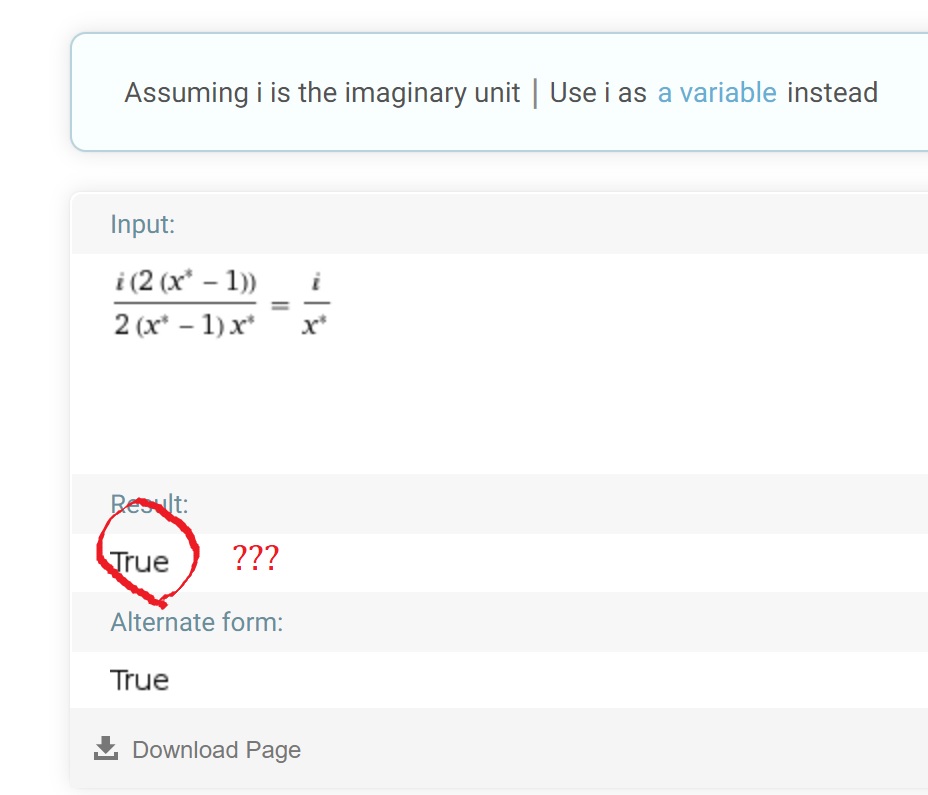
Is there an incorrect theorem embedded in wolfram alpha, or is this a bug? See image.
Any time I enter " (i (2 x^* - 1))/(2 (x^* - 1) x^* ) " it reduces to "i / x^* " I need to show an equivalence, but when this is on the right hand side of the equation, it reduces to this " i/x^* " nonsense. Any ideas? I see why it's doing it (order of operations), but it's wrong.