I think the main issue is that both models are overparameterized for the available data (and secondarily better starting values are needed). A plot of the data shows just slight curvature over values of
$t$ for both datasets suggesting that maybe just 3 parameters for each curve might be warranted. Or at least that having 6 parameters per curve is too much for the available data.
I want to emphasize that I'm not saying the models are wrong. It's just that the available data (meaning values of
$t$ from 0 to 10) doesn't allow for the estimation of all of the parameters. Maybe if there are more than two datasets, then more parameters might be able to be estimated.
Here is what works:
fit = MultiNonlinearModelFit[{dat1, dat2}, {model1[k3, k4, k5, ea1, eh1, ef1][t],
model2[k3, k4, k5, ea2, eh2, ef2][t]},
{{k3, 0.22}, {k4, 0}, {k5, 0}, {ea1, 6600}, {eh1, 6400}, {ef1, 0}, {ea2, 6200}, {eh2, 6000}, {ef2, 0}}, {t}];
mle = fit["BestFitParameters"]
(* {k3 -> 0.2188, k4 -> -5.24086, k5 -> 0., ea1 -> 6623.65,
eh1 -> 6364.94, ef1 -> 0.000336612, ea2 -> 6152.56, eh2 -> 5927.64, ef2 -> 0.000419775} *)
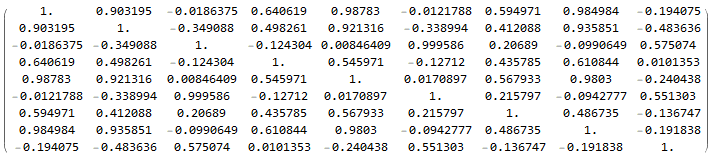
fit["CorrelationMatrix"] // MatrixForm
fit["ParameterTable"]
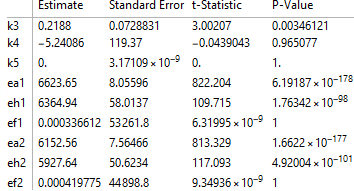
Note that the P-values suggest that k4, k5, ef1, and ef2 are not statistically significantly different from zero. However, the huge standard errors suggest that those parameters are not estimated very well. In short, there's not much one can say about those 4 parameters.
Show[ListPlot[{dat1, dat2}],
Plot[{model1[k3, 0, 0, ea1, eh1, 0][t] /. mle,
model2[k3, 0, 0, ea2, eh2, 0][t] /. mle}, {t, 0, 10}]]
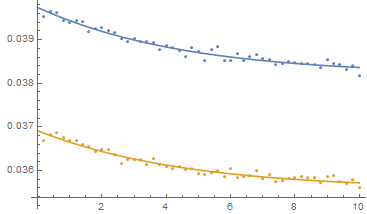
While MultiNonlinearModelFit is very handy for multiple datasets with common parameters, it does assume that the variability about the individual curves is the same (although with the Weight option one could allow for knowing that the variability is, say, twice as much in one dataset as another but I suspect that is a rare occurrence.) I think an explicit statement in the documentation about the assumption of the equality of the variances is warranted.