The intersection of the circular wavefronts and the beam waist can be solved for:

Clear[w0];
Clear[\[Lambda]];
sols = Solve[{(z - (zp - R[zp]))^2 + w^2 == R[zp]^2, (w/w0)^2 == 
     1 + ((\[Lambda] z)/(\[Pi] w0^2))^2}, {z, w}];
sols = {z, w} /. sols;
Last[sols]

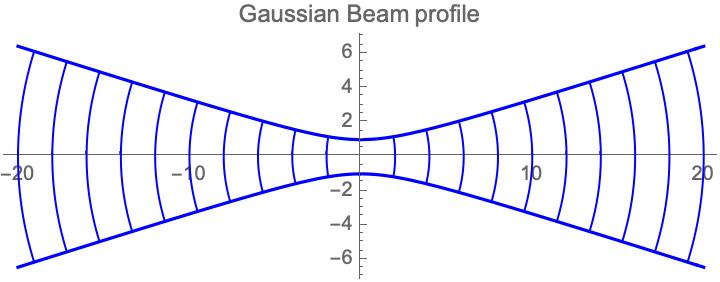
After which the wavefronts can be plotted:

zlim = 20;
w0 = 1;
\[Lambda] = 1.0;
w[z_] := w0*Sqrt[1 + ((\[Lambda] z)/(\[Pi] w0^2))^2];
R[z_] := z*(1 + ((\[Pi] w0^2)/(\[Lambda] z))^2);
zs[zp_] := (-2 \[Pi]^4 w0^6 + Sqrt[
   4 \[Pi]^8 w0^12 - 
    4 (-2 \[Pi]^4 w0^6 zp + \[Pi]^2 w0^4 zp \[Lambda]^2 - \[Pi]^2 \
w0^2 zp^3 \[Lambda]^2) (\[Pi]^2 w0^2 zp \[Lambda]^2 + 
       zp \[Lambda]^4)])/(
  2 (\[Pi]^2 w0^2 zp \[Lambda]^2 + zp \[Lambda]^4));
ws[zp_] := Sqrt[
  3 \[Pi]^2 w0^4 zp + zp^3 \[Lambda]^2 + (
   2 \[Pi]^6 w0^10)/(\[Pi]^2 w0^2 zp \[Lambda]^2 + 
    zp \[Lambda]^4) - (\[Pi]^2 w0^4 Sqrt[
    4 \[Pi]^8 w0^12 - 
     4 (-2 \[Pi]^4 w0^6 zp + \[Pi]^2 w0^4 zp \[Lambda]^2 - \[Pi]^2 \
w0^2 zp^3 \[Lambda]^2) (\[Pi]^2 w0^2 zp \[Lambda]^2 + 
        zp \[Lambda]^4)])/(\[Pi]^2 w0^2 zp \[Lambda]^2 + 
    zp \[Lambda]^4)]/Sqrt[\[Pi]^2 w0^2 zp + zp \[Lambda]^2];
\[Beta][zp_] := ArcSin[ws[zp]/(R[zp])];
zPoints = Select[Range[-zlim, zlim, zlim/10.], # != 0 &];
\[Beta]Bounds = \[Beta] /@ zPoints;
waveFronts = 
  MapThread[
   Circle[{#1 - R[#1], 0}, 
     Abs[R[#1]], ({-#2, #2} + 
       If[R[#1] < 0, \[Pi], 0])] &, {zPoints, \[Beta]Bounds}];
(*points=Point[{#,0}]&/@zPoints;*)
waistPlot = Plot[{w[z], -w[z]},
  {z, -zlim, zlim},
  PlotLabel -> Style["Gaussian Beam profile"],
  Epilog -> {Blue, waveFronts},
  AspectRatio -> Automatic,
  PlotStyle -> Blue]