I am sorry for the unclarity. Actually, I just wanted to find a way to
package a sub-network as a node and see what properties will the new
net have.
So you are having problems finding tooling to reshape graphs?
The tooling of WFPP is not really suitable for that as it based on the SetReplace primitive which match a fixed pattern of free variables against a (hyper-) graph. Consider this pattern:
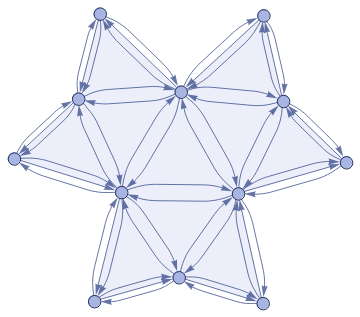
You see there are some nodes which have 2, 4, 6 neighbors. It is not a possible to write a rule in this framework which takes an arbitrary sub network and replaces it with a node and tie up all the out going connections to the new node. In fact you can't write a procedure which replaces any node creates a new node and ties it up in the same way as it was before.
The language of hyper-graph modifications in the WFPP is quiet restrictive. Your use case is to advanced for the current tooling, other places of the Wolfram language working on Graphs, not Hypergraphs are more suited for you. Furthermore i have not seen much interest in graph numbers other than dimensional of a local embedding.
And for the universes, I mean universes generated by different rules.
It is not only rules that matter but also initial state.