First, I need to resolve some confusion. Wolfram Physics Project is distinct from chapter 9 of NKS, and the model we now use is different. In particular, the state of the model is an unordered collection of edges, so using ReplaceAll or ReplaceList on them is not going to work.
Instead, the function you are looking for is WolframModel from the SetReplace package.
The question of whether the rule can be applied multiple times to the same place in a graph is an interesting one, and we did spend some time thinking about it in the past.
In the definition of the model we currently use, it can be applied multiple times, and each time a different b will be created, so you will get an evolution history that will look like this:
{{a, x}, {a, y}}
{{a, x}, {a, y}, {x, b$1}, {y, b$1}}
{{x, b$1}, {y, b$1}, {a, x}, {a, y}, {x, b$2}, {y, b$2}}
{{x, b$1}, {y, b$1}, {x, b$2}, {y, b$2}, {a, x}, {a, y}, {x, b$3}, {y, b$3}}
WolframModelPlot[{{x, b$1}, {y, b$1}, {x, b$2}, {y, b$2}, {a, x}, {a,
y}, {x, b$3}, {y, b$3}}, VertexLabels -> Automatic]
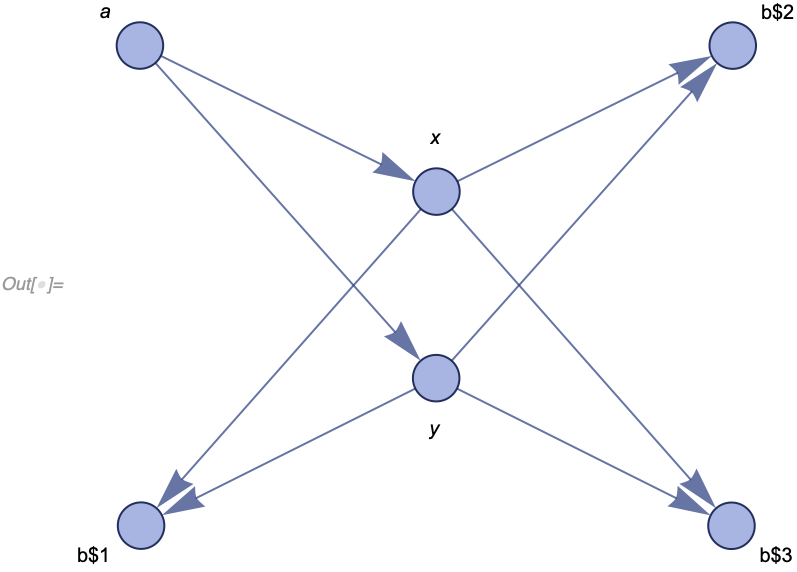 Notice that we are generating a new name for the new vertex every time, so multiple distinct copies of it can be created.
Notice that we are generating a new name for the new vertex every time, so multiple distinct copies of it can be created.
It can also be written explicitly as PatternRules as follows (note a Module on the right-hand side):
mathematica
WolframModel[<|
"PatternRules" -> {{a_, x_}, {a_, y_}} :>
Module[{b}, {{a, x}, {a, y}, {x, b}, {y, b}}]|>, {{a, x}, {a,
y}}, <|"MaxEvents" -> 3|>, "FinalStatePlot"]
However, one can imagine a different, "content-addressed" version of the model where the name for newly created vertices is chosen based on its predecessors, for example, as a hash of the input edges. In that case, while multiple copies of {x, b} and {y, b} will be created b will always correspond to the same vertex:
mathematica
WolframModel[<|
"PatternRules" -> {{a_, x_}, {a_, y_}} :>
Module[{b = Hash[{{a, x}, {a, y}}]}, {{a, x}, {a, y}, {x, b}, {y,
b}}]|>, {{a, x}, {a, y}}, <|
"MaxEvents" -> 3|>]["FinalStatePlot", VertexLabels -> Automatic]
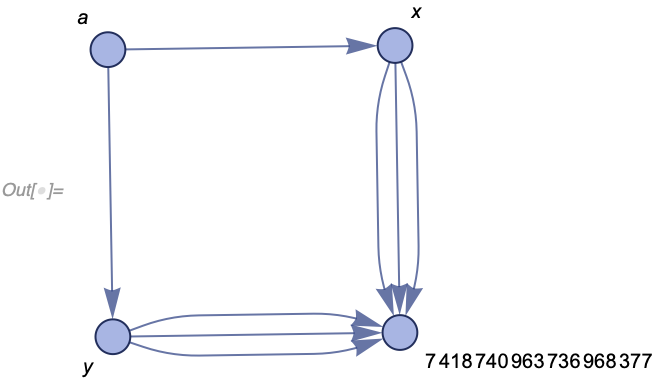
Finally, we could identify identical edges as well, in which case, we will get something similar to your second comment:
mathematica
WolframModelPlot[
Union[WolframModel[<|
"PatternRules" -> {{a_, x_}, {a_, y_}} :>
Module[{b = Hash[{{a, x}, {a, y}}]}, {{a, x}, {a, y}, {x,
b}, {y, b}}]|>, {{a, x}, {a, y}}, <|"MaxEvents" -> 3|>,
"FinalState"]], VertexLabels -> Automatic]
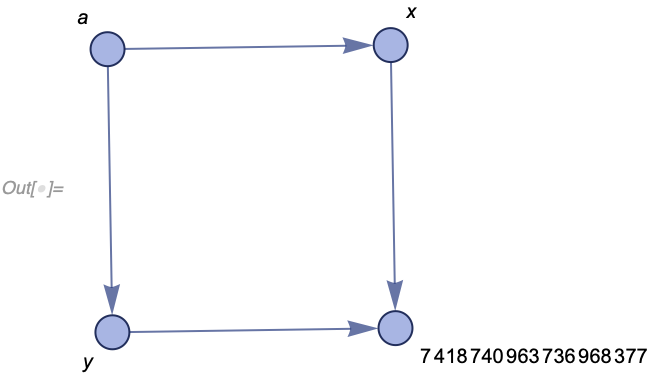
These three are just different models. And whether any one of them is a problem or a feature would depend on how well they reproduce known physics.
The issue #146 on GitHub is related to this.