I seek to define a 2d region and revolve it around a 3d parametric curve to make a solid, for exporting as an stl file. The curve can be seen in the ParametricPlot3D line below. The 2d region is not shown, but it's basically a segment of a ring centered on the curve, in the plane normal to the curve. I reason that the best way would be to define the 2d region in the first argument of RegionPlot3D, in terms of xyz distance from the curve in the plane normal to the curve, and run it from {t, 0, 34Pi}. The problem is that my function is defined parametrically in terms of t, not x,y,z, and RegionPlot3D demands x,y,z bounds. Any ideas?
xcoordinate[a_, b_, t_] := (a + b)*Cos[t] - b*Cos[(a + b)/b*t]
ycoordinate[a_, b_, t_] := (a + b)*Sin[t] - b*Sin[(a + b)/b*t]
zcoordinate[a_, b_, t_] := Sqrt[b^2 - ((b + a) - Sqrt[xcoordinate[a, b, t]^2 + ycoordinate[a, b, t]^2])^2]*
If[EvenQ[Floor[(a t)/(b \[Pi])]], 1, -1]
epicycloid = ParametricPlot[{xcoordinate[1/2, 17/14, t], ycoordinate[1/2, 17/14, t]}, {t, 0, 34 Pi}]
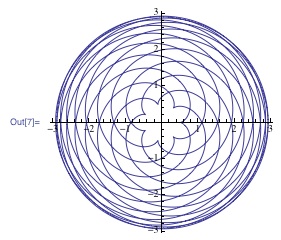
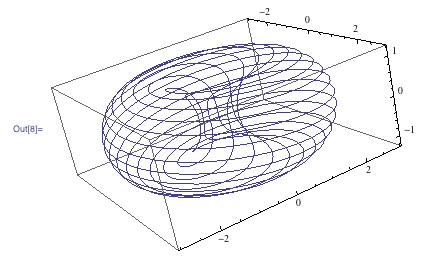
ParametricPlot3D[{xcoordinate[1/2, 17/14, t], ycoordinate[1/2, 17/14, t], zcoordinate[1/2, 17/14, t]}, {t, 0, 34 Pi}]
RegionPlot3D[
(Dot[{xcoordinate[a, b, t], ycoordinate[a, b, t], zcoordinate[a, b, t]} - {x, y, z}, {\!\(
\*SubscriptBox[\(\[PartialD]\), \(t\)]\(xcoordinate[a, b,
t]\)\), \!\(
\*SubscriptBox[\(\[PartialD]\), \(t\)]\(ycoordinate[a, b,
t]\)\), -If[EvenQ[Floor[(a t)/(b \[Pi])]], 1, -1] \!\(
\*SubscriptBox[\(\[PartialD]\), \(t\)]\(zcoordinate[a, b, t]\)\)}] ==
0)
\[And] (rcav <=
Norm[{x, y, z} - {xcoordinate[a, b, t], ycoordinate[a, b, t],
zcoordinate[a, b, t]}] <= (rcav + thickness))
\[And] other conditions,
{t, 0, 34 Pi}]
The sticky box garbles the code so here's a screenshot of that last input:
