I played a bit with evolution of multiway system to assembly a model of double-slit experiment slightly more literal than the one presented by Stephen and Jonathan in Working Session Thursday, Apr. 30, 2020 [Quantum Effects]. The result is some doubts about the possibility of representing QM with Wolfram model OR doubts in my fully understanding of this model and/or QM ;). I hope somebody will help me to see which option is closer to reality.

For start, as there are no available model of any physical particle yet, we need to assume that certain state represents particle of given position $x$. Let states be strings with "A" representing particle and "B" denoting positions where the particle is absent. The rules should allow particle to go left or right with the same probability.

Graph[ResourceFunction["MultiwaySystem"][{"A" -> "BA", "A" -> "AB"}, "A", 4, "EvolutionGraphFull", "IncludeStatePathWeights" -> True], VertexLabels -> "VertexWeight"]

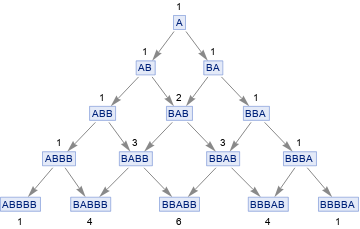
Since the probabilities of "particle" going left and right are equal, we get binomial distribution of state path weights, which tends to Gaussian as number of iteration increased. So far, so good - single "particle" spreads in Gaussian fashion as time progresses. Now we want to put a plate with two slits, to stop particle at certain positions from further propagation. It may be hard to define a rule for this, but we can simply remove states where "particle" is absorbed or reflected by the plate, since the result is the same - such states do not contribute to further evolution of the system. So we continue evolution with the same rules, but starting from two extreme states "ABBBB" and "BBBBA", as others are removed.

Graph[ResourceFunction["MultiwaySystem"][{"A" -> "BA", "A" -> "AB"}, {"ABBBB","BBBBA"}, 4, "EvolutionGraphFull", "IncludeStatePathWeights" -> True], VertexLabels -> "VertexWeight",VertexSize->Small]

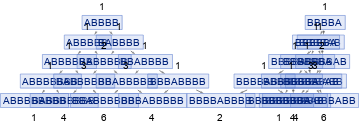
Apparently two trajectories begin to interfere, as both reach the same state "BBBBABBBB". The graph view becomes a bit messy, so let's switch to histogram view to check the actual interference pattern (in terms of state path weights) for higher number of iterations

evo =ResourceFunction["MultiwaySystem"][{"A" -> "BA", "A" -> "AB"}, {"ABBBB","BBBBA"}, 6,"AllStatesListUnmerged"];
count = KeySort[Counts[Last[evo]]];
BarChart[Values[count],ChartLabels->Placed[Keys[count],Axis, Rotate[#, Pi/2]&]]

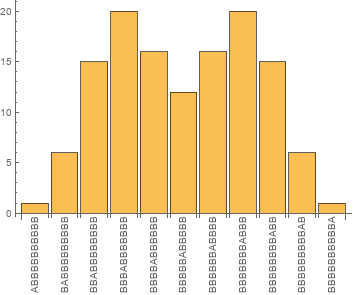
And here the trouble begins. Different branches of evolution indeed merge, but only in constructive manner. As a result we don't get quantum interference pattern, since has to include both constructive and destructive interferences. The central question is then: can we get such destructive interference assuming only causal invariance, i.e. mechanism of path convergence/merging branches? The presented experiment is extremely simplified, the proposed representation of particle state and/or used rules may be inadequate. But the property of evolution in multiway graph that I think should hold in the general case is that adding some obstacle for stopping particle propagation is equivalent to removing some states from the evolution (at the iteration corresponding to particle reaching this obstacle in the given branch). Obvious consequence is that for every state representing particle at position $x$ on the iteration $i$, its state path weight without any obstacle $W_{x,i}$ will be higher than weight for the same $x$ and $i$ with double slit plate, $W^{||}_{x,i}$, as in the latter case some paths are removed:

(1) $\forall x, W^{||}_{x,i} \leq W_{x,i}$.

But to reproduce double slit experiment we need more: state path weights for two slits have to be smaller than weights for only one open slit $W^|_{x,i}$, for some $x$ corresponding to destructive interference locations

(2) $\exists x, W^{||}_{x,i} < W^|_{x,i}$.

Actually for some $x,i$ we should even have $W^{||}_{x,i}=0$, as the interference is fully destructive. Now, how we can fulfill such condition if opening second slit can only increase the number of paths leading to each state? In other words, how can interference be destructive, as required in QM, if causal invariance appears to be only constructive? Am I missing something?