Here is a dataset:
data = {{0., 0.}, {1.*10^-7, 3.39166*10^9}, {2.*10^-7,
3.86908*10^9}, {3.*10^-7, 3.68845*10^9}, {4.*10^-7,
3.44633*10^9}, {5.*10^-7, 2.80581*10^9}, {6.*10^-7,
2.44311*10^9}, {7.*10^-7, 1.80159*10^9}, {8.*10^-7,
1.48215*10^9}, {9.*10^-7, 1.25664*10^9}, {1.*10^-6,
1.07927*10^9}, {1.1*10^-6, 9.31846*10^8}, {1.2*10^-6,
7.95327*10^8}, {1.3*10^-6, 7.09389*10^8}, {1.4*10^-6,
5.86299*10^8}, {1.5*10^-6, 4.83926*10^8}, {1.6*10^-6,
4.76692*10^8}, {1.7*10^-6, 4.99015*10^8}, {1.8*10^-6,
3.91846*10^8}, {1.9*10^-6, 4.14296*10^8}, {2.*10^-6,
3.80016*10^8}, {2.1*10^-6, 3.91943*10^8}, {2.2*10^-6,
4.08778*10^8}, {2.3*10^-6, 4.03334*10^8}, {2.4*10^-6,
3.89268*10^8}, {2.5*10^-6, 3.83273*10^8}, {2.6*10^-6,
4.04076*10^8}, {2.7*10^-6, 4.07262*10^8}, {2.8*10^-6,
4.82715*10^8}, {2.9*10^-6, 4.69429*10^8}, {3.*10^-6,
4.72035*10^8}, {3.1*10^-6, 4.65755*10^8}, {3.2*10^-6,
5.39881*10^8}, {3.3*10^-6, 5.1622*10^8}, {3.4*10^-6,
4.96533*10^8}, {3.5*10^-6, 5.93332*10^8}, {3.6*10^-6,
5.98046*10^8}, {3.7*10^-6, 6.02247*10^8}, {3.8*10^-6,
6.01825*10^8}, {3.9*10^-6, 6.10475*10^8}, {4.*10^-6,
5.63126*10^8}, {4.1*10^-6, 6.37773*10^8}, {4.2*10^-6,
6.81107*10^8}, {4.3*10^-6, 7.16579*10^8}, {4.4*10^-6,
6.50391*10^8}, {4.5*10^-6, 7.56059*10^8}, {4.6*10^-6,
7.16895*10^8}, {4.7*10^-6, 6.82833*10^8}, {4.8*10^-6,
7.89698*10^8}, {4.9*10^-6, 7.00052*10^8}, {5.*10^-6,
6.78524*10^8}, {5.1*10^-6, 7.28389*10^8}, {5.2*10^-6,
8.22536*10^8}, {5.3*10^-6, 7.91637*10^8}, {5.4*10^-6,
7.35369*10^8}, {5.5*10^-6, 7.32631*10^8}, {5.6*10^-6,
8.67581*10^8}, {5.7*10^-6, 8.23457*10^8}, {5.8*10^-6,
7.79288*10^8}, {5.9*10^-6, 8.95142*10^8}, {6.*10^-6,
8.4047*10^8}, {6.1*10^-6, 8.1395*10^8}, {6.2*10^-6,
8.39743*10^8}, {6.3*10^-6, 8.21923*10^8}, {6.4*10^-6,
8.05072*10^8}, {6.5*10^-6, 8.18719*10^8}, {6.6*10^-6,
9.23688*10^8}, {6.7*10^-6, 9.43367*10^8}, {6.8*10^-6,
8.77086*10^8}, {6.9*10^-6, 9.14967*10^8}, {7.*10^-6,
8.28941*10^8}, {7.1*10^-6, 9.07827*10^8}, {7.2*10^-6,
8.31515*10^8}, {7.3*10^-6, 9.09561*10^8}, {7.4*10^-6,
9.55785*10^8}, {7.5*10^-6, 9.85295*10^8}, {7.6*10^-6,
9.33683*10^8}, {7.7*10^-6, 9.68907*10^8}, {7.8*10^-6,
9.61543*10^8}, {7.9*10^-6, 9.04016*10^8}, {8.*10^-6,
8.71894*10^8}, {8.1*10^-6, 9.40331*10^8}, {8.2*10^-6,
1.04923*10^9}, {8.3*10^-6, 8.64988*10^8}, {8.4*10^-6,
1.05481*10^9}, {8.5*10^-6, 9.85464*10^8}, {8.6*10^-6,
1.05189*10^9}, {8.7*10^-6, 1.00359*10^9}, {8.8*10^-6,
9.72721*10^8}, {8.9*10^-6, 9.04025*10^8}, {9.*10^-6,
9.08352*10^8}, {9.1*10^-6, 1.04109*10^9}, {9.2*10^-6,
1.03116*10^9}, {9.3*10^-6, 1.02555*10^9}, {9.4*10^-6,
9.50933*10^8}, {9.5*10^-6, 1.01088*10^9}, {9.6*10^-6,
9.87032*10^8}, {9.7*10^-6, 1.00772*10^9}, {9.8*10^-6,
1.08818*10^9}, {9.9*10^-6, 1.06048*10^9}, {0.00001,
9.99967*10^8}, {0.0000101, 9.18289*10^8}, {0.0000102,
1.03644*10^9}, {0.0000103, 9.56547*10^8}, {0.0000104,
1.00228*10^9}, {0.0000105, 9.8047*10^8}, {0.0000106,
1.01173*10^9}, {0.0000107, 1.02315*10^9}, {0.0000108,
1.01858*10^9}, {0.0000109, 1.05174*10^9}, {0.000011,
1.04142*10^9}, {0.0000111, 9.00135*10^8}, {0.0000112,
9.80817*10^8}, {0.0000113, 1.07352*10^9}, {0.0000114,
1.05384*10^9}, {0.0000115, 9.2476*10^8}, {0.0000116,
8.99596*10^8}, {0.0000117, 1.05152*10^9}, {0.0000118,
9.93397*10^8}, {0.0000119, 1.07438*10^9}, {0.000012,
9.60509*10^8}, {0.0000121, 1.00689*10^9}, {0.0000122,
8.86177*10^8}, {0.0000123, 9.42264*10^8}, {0.0000124,
1.07192*10^9}, {0.0000125, 8.99794*10^8}, {0.0000126,
1.0713*10^9}, {0.0000127, 1.02981*10^9}, {0.0000128,
1.05154*10^9}, {0.0000129, 1.03091*10^9}, {0.000013,
1.03633*10^9}, {0.0000131, 9.344*10^8}, {0.0000132,
9.78137*10^8}, {0.0000133, 1.02357*10^9}, {0.0000134,
8.91679*10^8}, {0.0000135, 1.02303*10^9}, {0.0000136,
9.15482*10^8}, {0.0000137, 9.95348*10^8}, {0.0000138,
9.74778*10^8}, {0.0000139, 9.38048*10^8}, {0.000014,
9.04718*10^8}, {0.0000141, 1.0405*10^9}, {0.0000142,
8.88924*10^8}, {0.0000143, 1.0012*10^9}, {0.0000144,
9.33177*10^8}, {0.0000145, 9.4341*10^8}, {0.0000146,
9.71105*10^8}, {0.0000147, 9.4746*10^8}, {0.0000148,
8.43605*10^8}, {0.0000149, 9.06436*10^8}, {0.000015,
9.69338*10^8}, {0.0000151, 9.84955*10^8}, {0.0000152,
8.59725*10^8}, {0.0000153, 1.01143*10^9}, {0.0000154,
9.7259*10^8}, {0.0000155, 9.49174*10^8}, {0.0000156,
8.75113*10^8}, {0.0000157, 9.15336*10^8}, {0.0000158,
8.34557*10^8}, {0.0000159, 8.19971*10^8}, {0.000016,
9.30407*10^8}, {0.0000161, 9.67152*10^8}, {0.0000162,
8.94882*10^8}, {0.0000163, 8.0498*10^8}, {0.0000164,
9.23441*10^8}, {0.0000165, 9.45013*10^8}, {0.0000166,
8.72109*10^8}, {0.0000167, 8.61614*10^8}, {0.0000168,
8.09602*10^8}, {0.0000169, 9.57019*10^8}, {0.000017,
8.83699*10^8}, {0.0000171, 9.00854*10^8}, {0.0000172,
8.14076*10^8}, {0.0000173, 9.16164*10^8}, {0.0000174,
9.07748*10^8}, {0.0000175, 7.7702*10^8}, {0.0000176,
8.6286*10^8}, {0.0000177, 7.68435*10^8}, {0.0000178,
9.00765*10^8}, {0.0000179, 8.56466*10^8}, {0.000018,
8.18085*10^8}, {0.0000181, 8.21704*10^8}, {0.0000182,
7.91811*10^8}, {0.0000183, 8.0648*10^8}, {0.0000184,
7.5514*10^8}, {0.0000185, 8.26893*10^8}, {0.0000186,
7.95685*10^8}, {0.0000187, 7.6267*10^8}, {0.0000188,
8.41511*10^8}, {0.0000189, 7.73116*10^8}, {0.000019,
8.85894*10^8}, {0.0000191, 8.23475*10^8}, {0.0000192,
7.4034*10^8}, {0.0000193, 8.39648*10^8}, {0.0000194,
7.39315*10^8}, {0.0000195, 7.92872*10^8}, {0.0000196,
7.70605*10^8}, {0.0000197, 7.39371*10^8}, {0.0000198,
7.70492*10^8}, {0.0000199, 7.3976*10^8}, {0.00002,
7.83134*10^8}, {0.0000201, 8.09033*10^8}, {0.0000202,
7.38801*10^8}, {0.0000203, 7.21872*10^8}, {0.0000204,
8.4009*10^8}, {0.0000205, 7.98868*10^8}, {0.0000206,
7.46261*10^8}, {0.0000207, 8.06325*10^8}, {0.0000208,
7.89416*10^8}, {0.0000209, 8.03027*10^8}, {0.000021,
7.43581*10^8}, {0.0000211, 7.24888*10^8}, {0.0000212,
7.8333*10^8}, {0.0000213, 7.44078*10^8}, {0.0000214,
7.65244*10^8}, {0.0000215, 7.952*10^8}, {0.0000216,
7.28251*10^8}, {0.0000217, 7.23171*10^8}, {0.0000218,
6.80909*10^8}, {0.0000219, 7.9246*10^8}, {0.000022,
6.80741*10^8}, {0.0000221, 7.15944*10^8}, {0.0000222,
7.22896*10^8}, {0.0000223, 6.53636*10^8}, {0.0000224,
7.03381*10^8}, {0.0000225, 7.67074*10^8}, {0.0000226,
6.86757*10^8}, {0.0000227, 6.6035*10^8}, {0.0000228,
6.36654*10^8}, {0.0000229, 7.33639*10^8}, {0.000023,
7.31589*10^8}, {0.0000231, 6.98409*10^8}, {0.0000232,
6.44259*10^8}, {0.0000233, 6.35483*10^8}, {0.0000234,
6.37634*10^8}, {0.0000235, 6.48188*10^8}, {0.0000236,
7.31592*10^8}, {0.0000237, 6.34664*10^8}, {0.0000238,
6.73227*10^8}, {0.0000239, 7.10326*10^8}, {0.000024,
6.02693*10^8}, {0.0000241, 6.71917*10^8}, {0.0000242,
6.46444*10^8}, {0.0000243, 6.37423*10^8}, {0.0000244,
6.63044*10^8}, {0.0000245, 6.08254*10^8}, {0.0000246,
6.32155*10^8}, {0.0000247, 6.22086*10^8}, {0.0000248,
6.2532*10^8}, {0.0000249, 6.36542*10^8}, {0.000025,
5.79381*10^8}, {0.0000251, 6.66164*10^8}, {0.0000252,
5.70117*10^8}, {0.0000253, 6.11209*10^8}, {0.0000254,
6.05277*10^8}, {0.0000255, 5.93624*10^8}, {0.0000256,
6.16067*10^8}, {0.0000257, 5.99018*10^8}, {0.0000258,
6.57872*10^8}, {0.0000259, 6.30085*10^8}, {0.000026,
6.65799*10^8}, {0.0000261, 6.55413*10^8}, {0.0000262,
5.92113*10^8}, {0.0000263, 6.44564*10^8}, {0.0000264,
6.10029*10^8}, {0.0000265, 5.9371*10^8}, {0.0000266,
5.65377*10^8}, {0.0000267, 5.90883*10^8}, {0.0000268,
6.11637*10^8}, {0.0000269, 6.23212*10^8}, {0.000027,
6.17805*10^8}, {0.0000271, 5.38741*10^8}, {0.0000272,
5.83618*10^8}, {0.0000273, 6.0041*10^8}, {0.0000274,
5.56333*10^8}, {0.0000275, 5.13713*10^8}, {0.0000276,
5.12148*10^8}, {0.0000277, 5.30965*10^8}, {0.0000278,
5.60605*10^8}, {0.0000279, 5.2272*10^8}, {0.000028,
5.51127*10^8}, {0.0000281, 5.04168*10^8}, {0.0000282,
5.14178*10^8}, {0.0000283, 5.94454*10^8}, {0.0000284,
5.78721*10^8}, {0.0000285, 5.21788*10^8}, {0.0000286,
5.5241*10^8}, {0.0000287, 5.90208*10^8}, {0.0000288,
5.42099*10^8}, {0.0000289, 5.09665*10^8}, {0.000029,
5.45981*10^8}, {0.0000291, 5.26996*10^8}, {0.0000292,
5.0748*10^8}, {0.0000293, 5.71479*10^8}, {0.0000294,
5.31232*10^8}, {0.0000295, 5.59563*10^8}, {0.0000296,
5.56977*10^8}, {0.0000297, 5.61372*10^8}, {0.0000298,
5.0442*10^8}, {0.0000299, 5.4357*10^8}, {0.00003,
4.86132*10^8}, {0.0000301, 5.456*10^8}, {0.0000302,
5.34631*10^8}, {0.0000303, 5.4936*10^8}, {0.0000304,
5.34136*10^8}, {0.0000305, 5.24645*10^8}, {0.0000306,
4.54585*10^8}, {0.0000307, 4.58091*10^8}, {0.0000308,
4.87664*10^8}, {0.0000309, 4.55286*10^8}, {0.000031,
4.47551*10^8}, {0.0000311, 4.72437*10^8}, {0.0000312,
4.45435*10^8}, {0.0000313, 4.97613*10^8}, {0.0000314,
4.65671*10^8}, {0.0000315, 4.79391*10^8}, {0.0000316,
4.42831*10^8}, {0.0000317, 4.368*10^8}, {0.0000318,
4.65957*10^8}, {0.0000319, 4.50196*10^8}, {0.000032,
4.38162*10^8}, {0.0000321, 4.87768*10^8}, {0.0000322,
4.53381*10^8}, {0.0000323, 4.57529*10^8}, {0.0000324,
4.86794*10^8}, {0.0000325, 4.23186*10^8}, {0.0000326,
4.68862*10^8}, {0.0000327, 4.44758*10^8}, {0.0000328,
4.53327*10^8}, {0.0000329, 4.18544*10^8}, {0.000033,
4.10309*10^8}, {0.0000331, 4.50224*10^8}, {0.0000332,
4.37544*10^8}, {0.0000333, 4.62282*10^8}, {0.0000334,
4.29525*10^8}, {0.0000335, 3.97015*10^8}, {0.0000336,
4.69631*10^8}, {0.0000337, 4.6895*10^8}, {0.0000338,
4.71176*10^8}, {0.0000339, 4.62413*10^8}, {0.000034,
4.46579*10^8}, {0.0000341, 4.31258*10^8}, {0.0000342,
3.97241*10^8}, {0.0000343, 4.31504*10^8}, {0.0000344,
4.20072*10^8}, {0.0000345, 4.35695*10^8}, {0.0000346,
4.18587*10^8}, {0.0000347, 4.21074*10^8}, {0.0000348,
4.32613*10^8}, {0.0000349, 3.84042*10^8}, {0.000035,
3.86439*10^8}, {0.0000351, 4.29599*10^8}, {0.0000352,
4.11321*10^8}, {0.0000353, 4.02481*10^8}, {0.0000354,
4.40943*10^8}, {0.0000355, 3.81824*10^8}, {0.0000356,
4.37794*10^8}, {0.0000357, 3.83326*10^8}, {0.0000358,
3.72904*10^8}, {0.0000359, 3.73611*10^8}, {0.000036,
4.0818*10^8}, {0.0000361, 4.14224*10^8}, {0.0000362,
4.08557*10^8}, {0.0000363, 3.57366*10^8}, {0.0000364,
3.722*10^8}, {0.0000365, 3.51478*10^8}, {0.0000366,
4.24273*10^8}, {0.0000367, 3.98138*10^8}, {0.0000368,
3.98873*10^8}, {0.0000369, 4.07259*10^8}, {0.000037,
3.4828*10^8}, {0.0000371, 3.59175*10^8}, {0.0000372,
4.01442*10^8}, {0.0000373, 4.02545*10^8}, {0.0000374,
3.97001*10^8}, {0.0000375, 3.69695*10^8}, {0.0000376,
4.01087*10^8}, {0.0000377, 3.46884*10^8}, {0.0000378,
3.40665*10^8}, {0.0000379, 3.81782*10^8}, {0.000038,
3.85267*10^8}, {0.0000381, 3.93677*10^8}, {0.0000382,
3.4168*10^8}, {0.0000383, 3.40748*10^8}, {0.0000384,
3.28001*10^8}, {0.0000385, 3.73761*10^8}, {0.0000386,
3.61158*10^8}, {0.0000387, 3.87561*10^8}, {0.0000388,
3.633*10^8}, {0.0000389, 3.4367*10^8}, {0.000039,
3.29006*10^8}, {0.0000391, 3.63263*10^8}, {0.0000392,
3.64321*10^8}, {0.0000393, 3.18616*10^8}, {0.0000394,
3.37887*10^8}, {0.0000395, 3.71965*10^8}, {0.0000396,
3.64279*10^8}, {0.0000397, 3.38655*10^8}, {0.0000398,
3.53998*10^8}, {0.0000399, 3.69957*10^8}, {0.00004,
3.66599*10^8}, {0.0000401, 3.45273*10^8}, {0.0000402,
3.05927*10^8}, {0.0000403, 3.39315*10^8}, {0.0000404,
3.20745*10^8}, {0.0000405, 3.39915*10^8}, {0.0000406,
3.02635*10^8}, {0.0000407, 3.2508*10^8}, {0.0000408,
3.52145*10^8}, {0.0000409, 3.43104*10^8}, {0.000041,
3.55959*10^8}, {0.0000411, 3.05492*10^8}, {0.0000412,
2.94112*10^8}, {0.0000413, 3.1421*10^8}, {0.0000414,
3.16455*10^8}, {0.0000415, 3.48402*10^8}, {0.0000416,
3.40535*10^8}, {0.0000417, 3.38442*10^8}, {0.0000418,
3.2622*10^8}, {0.0000419, 3.34345*10^8}, {0.000042,
3.15076*10^8}, {0.0000421, 3.18726*10^8}, {0.0000422,
3.08504*10^8}, {0.0000423, 3.06754*10^8}, {0.0000424,
3.3602*10^8}, {0.0000425, 3.3578*10^8}, {0.0000426,
3.04322*10^8}, {0.0000427, 3.04005*10^8}, {0.0000428,
2.9239*10^8}, {0.0000429, 2.77703*10^8}, {0.000043,
3.00855*10^8}, {0.0000431, 3.03118*10^8}, {0.0000432,
2.73178*10^8}, {0.0000433, 3.10125*10^8}, {0.0000434,
3.24634*10^8}, {0.0000435, 2.85507*10^8}, {0.0000436,
3.0253*10^8}, {0.0000437, 2.94682*10^8}, {0.0000438,
2.67459*10^8}, {0.0000439, 2.78222*10^8}, {0.000044,
2.78228*10^8}, {0.0000441, 2.68133*10^8}, {0.0000442,
2.80897*10^8}, {0.0000443, 3.1133*10^8}, {0.0000444,
2.67488*10^8}, {0.0000445, 2.95369*10^8}, {0.0000446,
3.0872*10^8}, {0.0000447, 2.78099*10^8}, {0.0000448,
2.88453*10^8}, {0.0000449, 2.64087*10^8}, {0.000045,
2.53686*10^8}, {0.0000451, 2.78259*10^8}, {0.0000452,
2.55547*10^8}, {0.0000453, 3.03588*10^8}, {0.0000454,
2.65502*10^8}, {0.0000455, 2.94768*10^8}, {0.0000456,
2.83474*10^8}, {0.0000457, 2.81128*10^8}, {0.0000458,
2.63055*10^8}, {0.0000459, 2.5719*10^8}, {0.000046,
2.86383*10^8}, {0.0000461, 2.5114*10^8}, {0.0000462,
2.68705*10^8}, {0.0000463, 2.47606*10^8}, {0.0000464,
2.65907*10^8}, {0.0000465, 2.42737*10^8}, {0.0000466,
2.75109*10^8}, {0.0000467, 2.87195*10^8}, {0.0000468,
2.76994*10^8}, {0.0000469, 2.41292*10^8}, {0.000047,
2.58802*10^8}, {0.0000471, 2.37396*10^8}, {0.0000472,
2.54686*10^8}, {0.0000473, 2.3203*10^8}, {0.0000474,
2.3556*10^8}, {0.0000475, 2.52191*10^8}, {0.0000476,
2.73224*10^8}, {0.0000477, 2.52723*10^8}, {0.0000478,
2.66194*10^8}, {0.0000479, 2.31522*10^8}, {0.000048,
2.27543*10^8}, {0.0000481, 2.71421*10^8}, {0.0000482,
2.57852*10^8}, {0.0000483, 2.61125*10^8}, {0.0000484,
2.33866*10^8}, {0.0000485, 2.42181*10^8}, {0.0000486,
2.66695*10^8}, {0.0000487, 2.64178*10^8}, {0.0000488,
2.35225*10^8}, {0.0000489, 2.65588*10^8}, {0.000049,
2.48891*10^8}, {0.0000491, 2.45468*10^8}, {0.0000492,
2.28972*10^8}, {0.0000493, 2.6166*10^8}, {0.0000494,
2.39098*10^8}, {0.0000495, 2.39786*10^8}, {0.0000496,
2.21521*10^8}, {0.0000497, 2.18797*10^8}, {0.0000498,
2.20248*10^8}, {0.0000499, 2.13029*10^8}, {0.00005, 2.38022*10^8}}
I am trying to fit this dataset to a system of ODEs. Here are some constants:
(* init initital values *)
k1 = 10.*10^-10; (* Cs^++Cs\[Rule]Subsuperscript[Cs, 2, +] *)
k2 = 2.*10^-14; (* Cs^++Subscript[H, 2]\[Rule]CsH^++H *)
(*k3=1.00000000000000000000*10^-7; (* \!\(
\*SubsuperscriptBox[\(Cs\), \(2\), \(+\)] + e\)\[Rule]Cs*+Cs(6s) *)*)
k5 = 1.*10^7; (* Cs* \[Rule]Cs(6s)+hv' *)
kp = 8.*10^-10; (* NOT SURE Cs*\[Rule]Cs(6s)+hv *)
f = 0.95; (* *)
kr1 = 1.*10^6; (* Cs(7p)\[Rule]Cs(6s)+hv *)
nH2 = 1.5*10^18; (* *)
Here is the ODE and fit Code:
tmax = 5.*10*10^-5;
ode =
{
(* Cs(6s) *)
Derivative[1][n0][t] ==
kr1*nhv[t] - k1*n0[t]*n1[t] + k5*n2[t] +
k3*(nCsH[t] + nCs2[t])*ne[t] + kp*nhv[t]^2,
(* Cs(7p) *)Derivative[1][nhv][t] == -(kr1 + 2*kp*nhv[t])*nhv[t],
(* edensity *)
Derivative[1][ne][t] == -k3*(nCs2[t] + nCsH[t])*ne[t] +
kp*f*nhv[t]^2,
(* Subsuperscript[Cs, 2, +] *)
Derivative[1][nCs2][t] == k1*n1[t]*n0[t] - k3*ne[t]*nCs2[t],
(* Cs^* *)
Derivative[1][n2][t] ==
k3*nCs2[t]*ne[t] - k5*n2[t] + kp*(1 - f)*nhv[t]^2,
(* CsH^+ *)
Derivative[1][nCsH][t] == k2*n1[t]*nH2 - k3*nCsH[t]*ne[t],
(* Cs^+ *)
Derivative[1][n1][t] == f*kp*nhv[t]^2 - (k1*n0[t] + k2*nH2)*n1[t],
n0[0] == 4.*10^13,(* Cs(6s) *)
n1[0] == 0.,
nhv[0] == 4.*10^13,
ne[0] == 0.,
nCs2[0] == 0.,
nCsH[0] == 0.,
n2[0] == 0.
};
paramSOL = ParametricNDSolve(*Value*)[
ode,
{n0, nhv, n1, n2, nCs2, nCsH, ne},
{t, 0., tmax},
{k3},
(*Method\[Rule]{NMinimize,Method\[Rule]"DifferentialEvolution"},*)
Method -> "StiffnessSwitching",
AccuracyGoal -> 10
]
{n0Func, n1Func, nhvFunc, neFunc, nCs2Func, nCsHFunc,
n2Func} = {n0, n1, nhv, ne, nCs2, nCsH, n2} /. paramSOL
model[k3_][t_] := n2Func[k3][t]
fit = NonlinearModelFit[
random, {n2Func[k3][t], 0.5*10.^-8 < k3 < 1.4*10.^-5}, {k3},
t]; // Timing
With this, the calculation is finding k3. I simulated the data and gave it some randomness, and then took away the k3 value to have the computer find it. It takes about 120 seconds, which is fine for 1 parameter, but when I take away a second parameter to have it fit 2 parameters, it takes hours. I would like to be able to solve for 3 parameters in a reasonable amount of time.
Parallelization does not seem to help (i mean this is fitting only 1 parameter so that makes sense), and I have tried some different settings, but overall nothing I have done has significantly increased the speed of the optimization procedure. 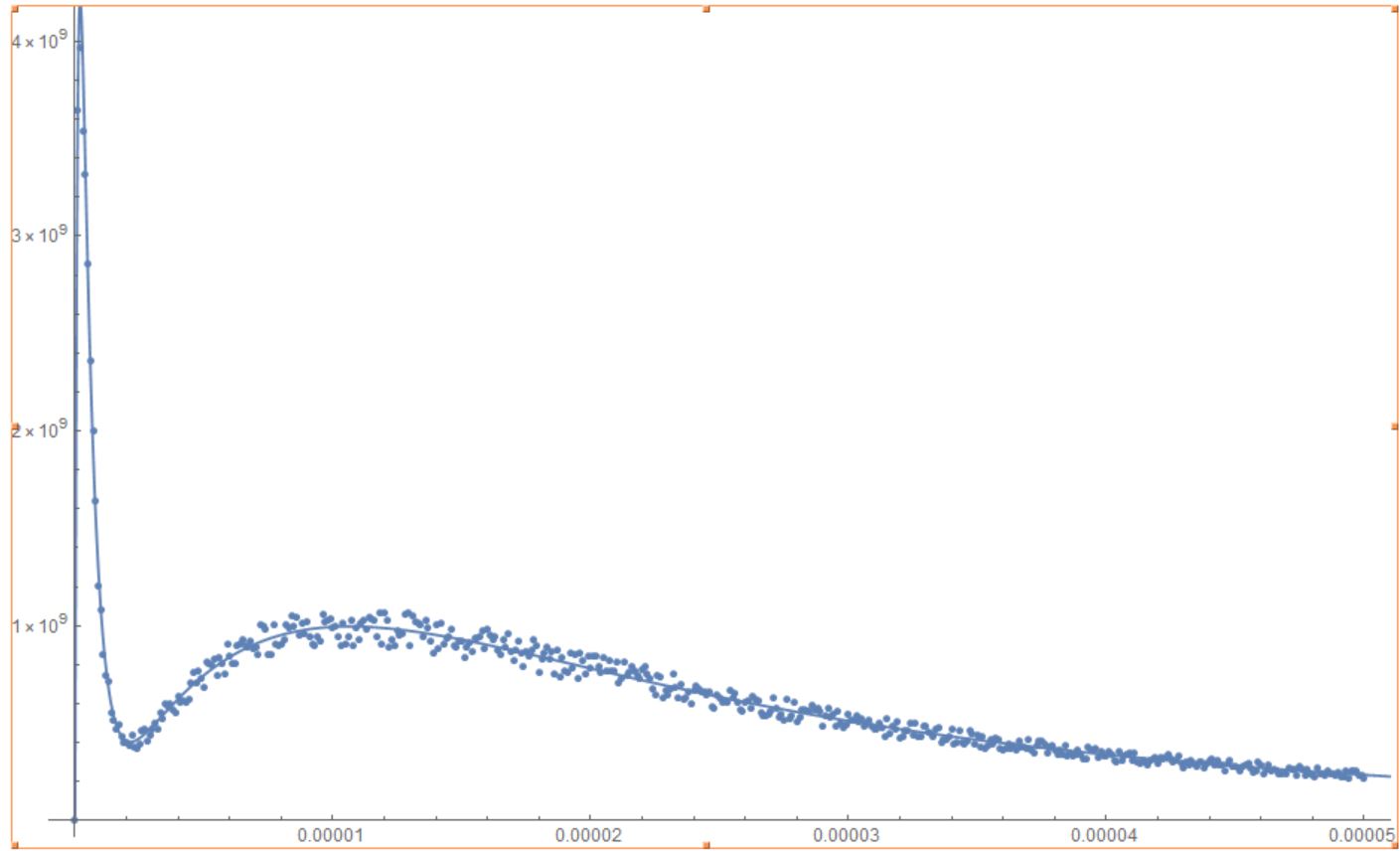 Advice?
Advice?