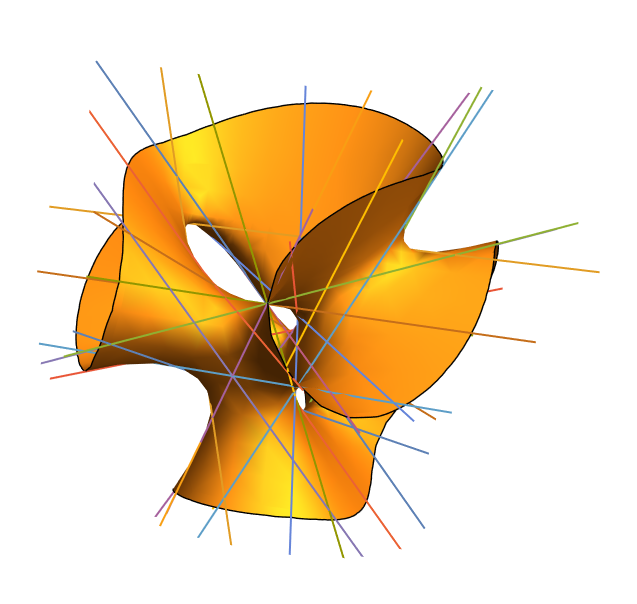
OK, I found the parameters of the lines on this nice site. In the most simple way one can show them like so:
l1 = {{1, \[Minus]1, 0} t + {0, 0, \[Minus]1/3},
{1, 0, \[Minus]1} t + {0, \[Minus]1/3, 0},
{0, 1, \[Minus]1} t + {\[Minus]1/3, 0, 0},
{1, \[Minus]1, 0} t + {1/6, 1/6, 0},
{1, \[Minus]1, 0} t + {1/3, 1/3, 1/3},
{1, 0, \[Minus]1} t + {1/6, 0, 1/6},
{1, 0, \[Minus]1} t + {1/3, 1/3, 1/3},
{0, 1, \[Minus]1} t + {0, 1/6, 1/6},
{0, 1, \[Minus]1} t + {1/3, 1/3, 1/3},
{3, 0, 1} t + {1/6, 0, 1/6},
{3, 1, 0} t + {1/6, 1/6, 0},
{0, 3, 1} t + {0, 1/6, 1/6},
{1, 3, 0} t + {1/6, 1/6, 0},
{0, 1, 3} t + {0, 1/6, 1/6},
{1, 0, 3} t + {1/6, 0, 1/6}};
l2 = {{1 + 3/Sqrt[5], \[Minus](1/Sqrt[5]), 1} t + {(5 + Sqrt[5])/
30, (5 + 3 Sqrt[5])/30, 0},
{\[Minus](1/Sqrt[5]), 1 + 3/Sqrt[5], 1} t + {(5 + 3 Sqrt[5])/
30, (5 + Sqrt[5])/30, 0},
{\[Minus]3 - Sqrt[5], \[Minus]Sqrt[5], 1} t + {(7 + 3 Sqrt[5])/
6, (3 + Sqrt[5])/6, 0},
{(\[Minus]3 + Sqrt[5])/4, (\[Minus]5 + 3 Sqrt[5])/4,
1} t + {(3 + Sqrt[5])/12, (1 - Sqrt[5])/12, 0},
{(\[Minus]5 - 3 Sqrt[5])/4, (\[Minus]3 - Sqrt[5])/4,
1} t + {(1 + Sqrt[5])/12, (3 - Sqrt[5])/12, 0},
{Sqrt[5], \[Minus]3 + Sqrt[5], 1} t + {(3 - Sqrt[5])/
6, (7 - 3 Sqrt[5])/6, 0},
{\[Minus]Sqrt[5], \[Minus]3 - Sqrt[5], 1} t + {(3 + Sqrt[5])/
6, (7 + 3 Sqrt[5])/6, 0},
{(\[Minus]5 + 3 Sqrt[5])/4, (\[Minus]3 + Sqrt[5])/4,
1} t + {(1 - Sqrt[5])/12, (3 + Sqrt[5])/12, 0},
{(\[Minus]3 - Sqrt[5])/4, (\[Minus]5 - 3 Sqrt[5])/4,
1} t + {(3 - Sqrt[5])/12, (1 + Sqrt[5])/12, 0},
{\[Minus]3 + Sqrt[5], Sqrt[5], 1} t + {(7 - 3 Sqrt[5])/
6, (3 - Sqrt[5])/6, 0},
{1/Sqrt[5], 1 - 3/Sqrt[5], 1} t + {(5 - 3 Sqrt[5])/
30, (5 - Sqrt[5])/30, 0},
{1 - 3/Sqrt[5], 1/Sqrt[5], 1} t + {(5 - Sqrt[5])/
30, (5 - 3 Sqrt[5])/30, 0}};
lines = Join[l1, l2];
plines = ParametricPlot3D[Evaluate@lines, {t, -1, 1}];
clebsch[x_, y_, z_] :=
81 (x^3 + y^3 + z^3) -
189 (x^2*y + x^2 z + y^2 x + y^2 z + z^2 x + z^2 y) + 54 (x y z) +
126 (x y + x z + y z) - 9 (x^2 + y^2 + z^2) - 9 (x + y + z) + 1
cl3D = ContourPlot3D[
clebsch[x, y, z] == 0, {x, y, z} \[Element] Ball[{0, 0, 0}, 1],
RegionBoundaryStyle -> None, Mesh -> None, Boxed -> False,
Axes -> False];
Show[cl3D, plines]