Group Abstract Group Abstract

Message Boards Message Boards

0
|
5.3K Views
|
10 Replies
|
1 Total Like
View groups...
Share
Share this post:

Definition of derivatives using Limit : D[f[x]=Limit(( f{x+h) - f(x) )/h ]

Abraham Gadalla
Posted 5 years ago

Definition of derivatives using Limit : D[f[x]=Limit(( f{x+h) - f(x) )/h ] as h approaches zero.

Given f[x_]:=PieceWise[{{x^3,-4<==x<==1}},{3x,x>1}];

Show using the definition of Limit that that D[f[x],x] is not defined at x = 1
POSTED BY: Abraham Gadalla
10 Replies
Sort By:

Thank you Rohit,

I greatly appreciate your response. The function is defined at x = -4, why is d[x] is not defined at -4? Why is d[-4] or f'[-4] is indeterminate? There is a discontinuity at x = 1, but what about at x = -4 It is defined.
POSTED BY: Abraham Gadalla
Rohit Namjoshi
Rohit Namjoshi
Posted 5 years ago

Hi Abraham,

There is a discontinuity at x = 1, but what about at x = -4 It is defined.

There is also a discontinuity at x = -4

Plot[{f[x](*,Evaluate@d[x]*)}, {x, -5, -3},
 PlotLabels -> "Expressions",
 ImageSize -> Large]

enter image description here

If a function is defined at x it does not imply that its derivative is defined at x. Take a look at the free Wolfram U course Introduction to Calculus. It covers these topics in Section 1 & 2.
POSTED BY: Rohit Namjoshi
Rohit Namjoshi
Rohit Namjoshi
Posted 5 years ago

Hey Abraham,

Plots are very useful for visualizing the behavior of functions.

ClearAll@f;
f[x_] := Piecewise[{{x^3, -4 <= x <= 1}, {3 x, x > 1}}]
d[x_] := Limit[(f[x + h] - f[x])/h, h -> 0]

Plot[{f[x], Evaluate@d[x]}, {x, 0, 2},
 PlotLabels -> "Expressions",
 ImageSize -> Large]

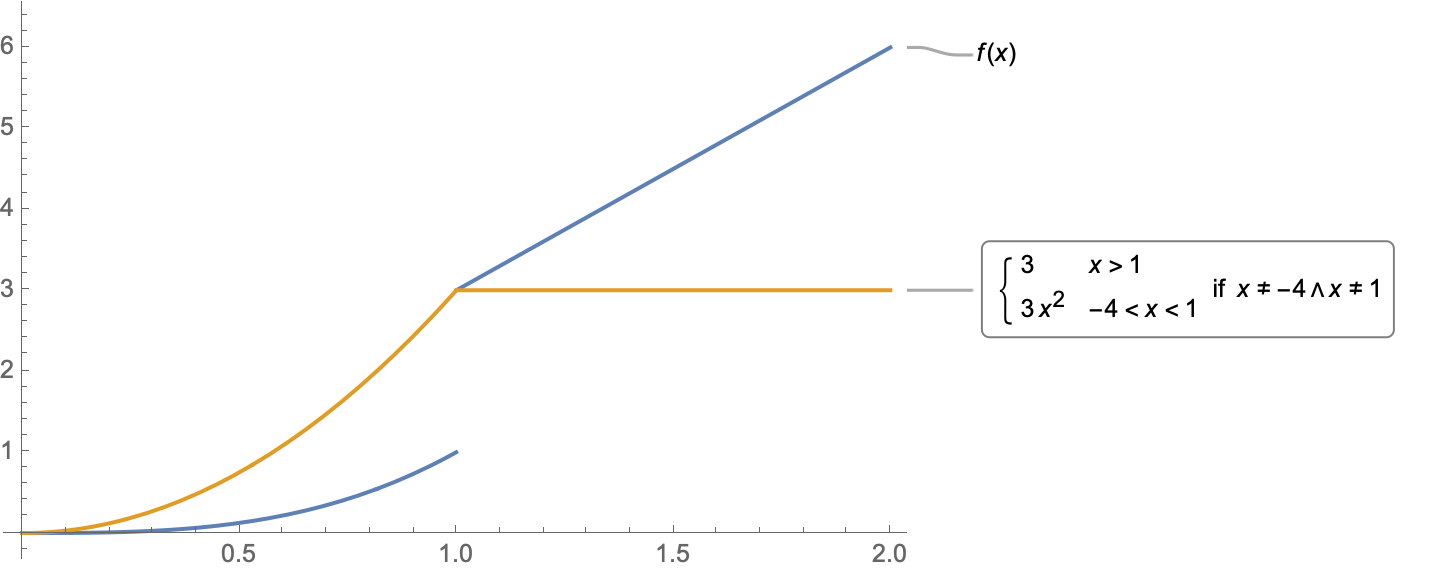
enter image description here

Note that d[x] is a ConditionalExpression that is not defined at x = 1 and x = -4

d[1]
(* Indeterminate *)

Or

Limit[(f[x + h] - f[x])/h, h -> 0] /. x -> 1
(* Undefined *)

Verify

f'[1]
(* Indeterminate] *)
POSTED BY: Rohit Namjoshi

Thank you for your reply,

It is clear that at x = 1, the function is defined x^3 =1, where as 3x is not defined at x =1 Yes, there is a discontinuity at x = 1 and we have two tangent parallel lines with a slope = 3. I guess, the question was how to use the definition of the limit to show that the derivative of x at the discontinuity point (here x = 1) is not defined.
POSTED BY: Abraham Gadalla

You are right! It should have been: ff2[x_] = Limit[((3 (x + a) - 3 x))/a, a -> 1] And the answer came to be: -3 x + 3(1+x) which after simplification is equal to 3
POSTED BY: Abraham Gadalla
Rohit Namjoshi
Rohit Namjoshi
Posted 5 years ago

Look at Plot[f[x], {x, 0, 2}]. There is a discontinuity at x = 1. Look at Limit[(f[x + h] - f[x])/h, h -> 0].

POSTED BY: Rohit Namjoshi

In addition to the typography issues noted by @RohitNamjoshi, there is trouble in the definition of 'f2'.
POSTED BY: Daniel Lichtblau
Rohit Namjoshi
Rohit Namjoshi
Posted 5 years ago

Piecewise, not PieceWise, -4 <= x <= 1, not -4<==x<==1.
POSTED BY: Rohit Namjoshi 
f[x_]:=PieceWise[{{x^3,-4<==x<==1}},{3x,x>1}];

f1[x_]=Limit[ ( (x+h)^3-x^3)/h, h->0];

f1[1] =3
f2[x_] = Limit[((3 (x + a) - 3 a))/(x - a), x -> a]

Indeterminate
POSTED BY: Abraham Gadalla
Rohit Namjoshi
Rohit Namjoshi
Posted 5 years ago

This looks like a question from the WolframU calculus course. What have you tried?
POSTED BY: Rohit Namjoshi
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard