Group Abstract Group Abstract

Message Boards Message Boards

0
|
7.7K Views
|
5 Replies
|
1 Total Like
View groups...
Share
Share this post:

Number of paths from Start to End through each node

Les Servi
Posted 5 years ago

Given an acyclic network g I am trying to figure out how to compute the number of paths in g going from the Start vertex to the End vertex through each vertex, i, in the network.

The closest function I found is BetweennessCentrality[g]. This looks at all pairs of start and end vertex and finds the fraction of the 'shortest paths' which goes through a vertex,i, of interest. This is close to what I want and shows that the basic functionality of computing number of paths through a vertex exists within Mathematica.

However, this isn't what I am looking for as I am not not interested in all possible start and end nodes and I am not interested in just shortest paths.

thx
POSTED BY: Les Servi
5 Replies
Sort By:
Les Servi
Les Servi
Posted 5 years ago

To clarify my question, for a given vertex, i I want to know how many paths from Start to End exists which goes through vertex i.

I see that FindPath can list all of the paths for me but I don't know how to count the number of the paths which contain i.

Also, what I really want to know is which nodes have the highest count, ie I want to do this for all nodes, i, and then sort the count.
POSTED BY: Les Servi
Rohit Namjoshi
Rohit Namjoshi
Posted 5 years ago

Hi Les,

It is not clear exactly what you are after. Let's use a specific example

g = ExampleData[{"NetworkGraph", "Friendship"}]

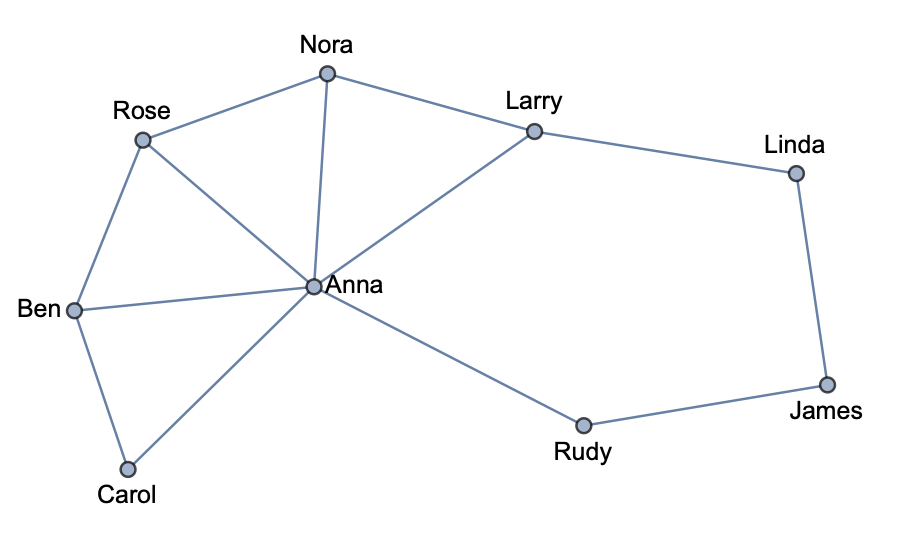
enter image description here

All paths between "Ben" and "James"

pathsBenJames = FindPath[g, "Ben", "James", Infinity, All]
(*
{{"Ben", "Anna", "Rudy", "James"}, {"Ben", "Carol", "Anna", "Rudy", 
  "James"}, {"Ben", "Rose", "Anna", "Rudy", "James"}, {"Ben", "Anna", 
  "Larry", "Linda", "James"}, {"Ben", "Carol", "Anna", "Larry", 
  "Linda", "James"}, {"Ben", "Rose", "Nora", "Larry", "Linda", 
  "James"}, {"Ben", "Rose", "Nora", "Anna", "Rudy", "James"}, {"Ben", 
  "Rose", "Anna", "Larry", "Linda", "James"}, {"Ben", "Anna", "Nora", 
  "Larry", "Linda", "James"}, {"Ben", "Carol", "Anna", "Nora", 
  "Larry", "Linda", "James"}, {"Ben", "Rose", "Nora", "Larry", "Anna",
   "Rudy", "James"}, {"Ben", "Rose", "Nora", "Anna", "Larry", "Linda",
   "James"}, {"Ben", "Rose", "Anna", "Nora", "Larry", "Linda", 
  "James"}, {"Ben", "Anna", "Rose", "Nora", "Larry", "Linda", 
  "James"}, {"Ben", "Carol", "Anna", "Rose", "Nora", "Larry", "Linda",
   "James"}}
*)

How many are there?

Length@pathsBenJames
(* 15 *)

Which paths include "Rudy"

pathsRudy = pathsBenJames // Select[MemberQ[#, "Rudy"] &]
(*
{{"Ben", "Anna", "Rudy", "James"}, {"Ben", "Carol", "Anna", "Rudy", 
  "James"}, {"Ben", "Rose", "Anna", "Rudy", "James"}, {"Ben", "Rose", 
  "Nora", "Anna", "Rudy", "James"}, {"Ben", "Rose", "Nora", "Larry", 
  "Anna", "Rudy", "James"}}
*)

Length@pathsRudy
(* 5 *)

Length of each path

Length /@ pathsRudy
(* {4, 5, 5, 6, 7} *)

I think that answers your first question, right?

Using the above example, can you explain what you mean by

Also, what I really want to know is which nodes have the highest count, ie I want to do this for all nodes, i, and then sort the count.
POSTED BY: Rohit Namjoshi
Les Servi
Les Servi
Posted 5 years ago

Thanks for your reply but ... for an acyclic graph

(1) there are typically many paths between two vertices, (See FindPath documentation of Mathematics) (2) Most of these paths will not be the shortest path
POSTED BY: Les Servi

Given that the graph g is acyclic, there is one and only one path between any two vertices. The path is necessarily the shortest path, and in general will not include every vertex.

I think you need to reconsider the your problem more carefully, and then you will find the solution.
POSTED BY: Robert Nachbar
Les Servi
Les Servi
Posted 5 years ago

What you wrote is true if the Start vertex and the Edge vertex are part of the same edge
POSTED BY: Les Servi
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard