I'm using the latest version, Mathematica 12.1.1.0 on Windows.
I've been doing some work with NDSolve involving coupled differential equations, and it hasn't behaved as I would have expected. I've got x'=f(x,y) and y'=g(x,y), and I'm finding that the variation in y is not feeding back into x' as I think it ought to, i.e. x' seems to be insensitive to the changes in y even though it's supposed to depend on y. In the course of investigating this, I have got it down to a very simple situation where I have got one variable, x, and I make x' depend on t. This also does not behave as I would expect. Specifically, I have
eqns = {
x'[t] == If[OddQ[Floor[t/10]], 1, -1],
x[0] == 0
};
soln = NDSolve[eqns, {x[t]}, {t, 0, 100}];
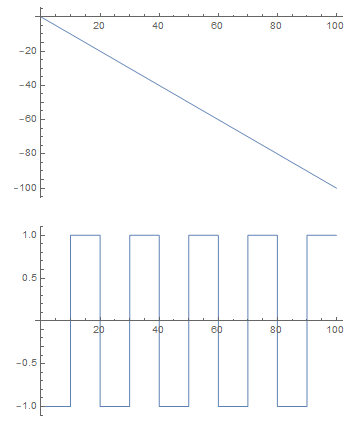
I would expect this to generate a sawtooth. x should increase with slope 1 when time is an odd multiple of 10 and decrease with slope -1 when time is an even multiple of 10.
But what I get is that x just decreases with constant slope -1. The first plot below is of
Plot[Evaluate[x[t] /. First[soln]], {t, 0, 100}]
which does not display the expected sawtooth, and the second plot below is of
OddQ[Floor[t/10]]
which does switch between 1 and -1 as expected.
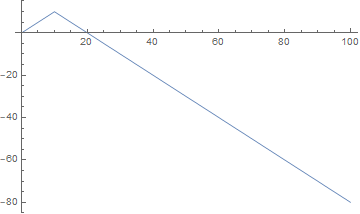
If I use a one-off switch in the value of x', so that it changes from 1 to -1 as t goes from below 10 to above 10, i.e.
eqns = {
x'[t] == If[Floor[t/10] < 1, 1, -1],
x[0] == 0
};
soln = NDSolve[eqns, {x[t]}, {t, 0, 100}];
Plot[Evaluate[x[t] /. First[soln]], {t, 0, 100}]
Then I get the behaviour I'd expect...
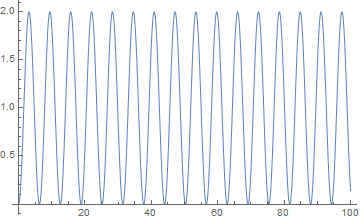
Similarly, if I make the driving of x' sinusoidal, I also get the behaviour I'd expect...
eqns = {
x'[t] == Sin[t],
x[0] == 0
};
soln = NDSolve[eqns, {x[t]}, {t, 0, 100}];
Plot[Evaluate[x[t] /. First[soln]], {t, 0, 100}]
results in...
So why doesn't the initial square wave driving and expected sawtooth for x work? Is this a bug, or an expected limitation of NDSolve? Or is there something I am missing?
This is disturbing because I don't know whether the unexpected behaviour of what I'm actually trying to model is a problem with my model or a problem with NDSolve.