How can I program the following problem into Mathematica?

$X,Y$ are i.i.d. Exponentially distributed random variables. Such that $X\sim\exp(1), \ Y\sim\exp(1)$. All other variables are positive real-valued.

The problem is to find $\Phi$ below. First, can anyone suggest if my approach to solving the expression on the right-hand side is correct? Using this approach, I stopped at Eq. (1) and then used Mathematica to further solve the expression.

My Mathematica Code is as below.

Egx = Expectation[(B*(1 + E^\[CurlyPhi]/E^(c*X)))/(a*b - D*(1 + E^\[CurlyPhi]/E^(c*X))), 
     Distributed[X, ExponentialDistribution[1]]]
Probability[Y >= Egx, Y \[Distributed] ExponentialDistribution[1]]

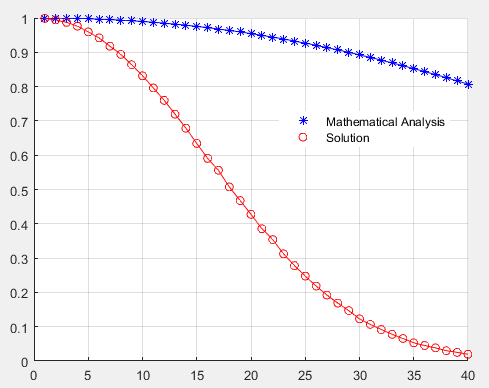
The Simulation and Analytical results do not match as shown in the image below.